
题目列表(包括答案和解析)
| 1 | 3 |
把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小1份是( )
是较小的两份之和,则最小1份是( )
A. 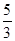 B.
B. C.
C.  D.
D. 
| 1 |
| 3 |
 等于较少的两份之和,则最少的一份面包个数是 .
等于较少的两份之和,则最少的一份面包个数是 . 等于较少的两份之和,则最少的一份面包个数是________.
等于较少的两份之和,则最少的一份面包个数是________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com