
题目列表(包括答案和解析)
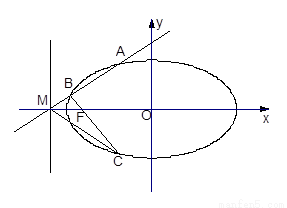
(本题满分12分)已知椭圆W的中心在原点,焦点在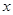 轴上,离心率为
轴上,离心率为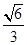 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为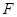 ,过左准线与
,过左准线与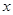 轴的交点
轴的交点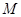 任作一条斜率不为零的直线
任作一条斜率不为零的直线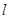 与椭圆W交于不同的两点
与椭圆W交于不同的两点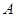 、
、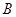 ,点
,点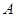 关于
关于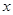 轴的对称点为
轴的对称点为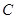 .
.
(Ⅰ)求椭圆W的方程;
(Ⅱ)求证: (
(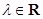 );
);
(本题满分12分)
为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?w.w.w.k.s.5.u.c.o.m ![]()
|
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(本题满分12分) 已知数列{an}满足![]()
(Ⅰ)求数列的前三项:a1,a2,a3;
(Ⅱ)求证:数列{![]() }为等差数列. w.w.w.k.s.5.u.c.o.m
}为等差数列. w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅲ)求数列{an}的前n项和Sn.
(本题满分12分)已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在x=1处的切线![]() 不过第四象限且斜率为3,又坐标原点到切线
不过第四象限且斜率为3,又坐标原点到切线![]() 的距离为
的距离为![]() ,若x=
,若x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a、b、c的值;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求y=f(x)在[-3,1]上的最大值和最小值.
(本题满分12分)已知{ }(
}( 是正整数)是首项是
是正整数)是首项是 ,公比是
,公比是 的等比数列
的等比数列 w_w w. k#s5_u.c o
w_w w. k#s5_u.c o
⑴求和: ;
; ;
;
⑵由(1)的结果归纳概括
并加以证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com