练习册

  • 练习册
  • 试题
    (三)解答题: 求出一个数学问题的正确结论后.将其作为条件之一.提出与原来问题有关的新问题.我们把它称为原来问题的一个“逆向 问题 例如.原来问题是“若正四棱锥底面边长为4.侧棱长为3.求该正四棱锥的体积 求出体积后.它的一个“逆向 问题可以是“若正四棱锥底面边长为4.体积为.求侧棱长 ,也可以是“若正四棱锥的体积为.求所有侧面面积之和的最小值 试给出问题“在平面直角坐标系中.求点到直线的距离 的一个有意义的“逆向 问题.并解答你所给出的“逆向 问题 注:(ⅰ) 在本题的解答过程中.如果考生所给问题的意义不大.那么在评分标准的第二阶段所列6分中.应只给2分.但第三阶段所列4分由考生对自己所给问题的解答正确与否而定 (ⅱ) 当考生所给出的“逆向 问题与所列解答不同.可参照所列评分标准的精神进行评分 [解] 点到直线的距离为 -- 4分 “逆向 问题可以是: (1) 求到直线的距离为2的点的轨迹方程 -- 10分 [解] 设所求轨迹上任意一点为.则. 所求轨迹为或 -- 14分 (2) 若点到直线的距离为2.求直线的方程 -- 10分 [解] .化简得.或. 所以.直线的方程为或 -- 14分 意义不大的“逆向 问题可能是: (3) 点是不是到直线的距离为2的一个点? -- 6分 [解] 因为. 所以点是到直线的距离为2的一个点 --10分 (4) 点是不是到直线的距离为2的一个点? -- 6分 [解] 因为. 所以点不是到直线的距离为2的一个点 --10分 (5) 点是不是到直线的距离为2的一个点? -- 6分 [解] 因为. 所以点不是到直线的距离为2的一个点 --10分 【查看更多】

     

    题目列表(包括答案和解析)

    三、解答题：本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.

    17.(本小题满分10分）

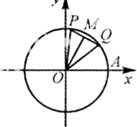
    如图，P，Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发，沿逆时针方向作匀角速度运动,其角速度分别为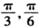（单位：弧度/秒）,M为线段PQ的中点，记经过x秒后(其中),

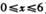    (I)求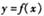的函数解析式；

     (II)将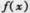图象上的各点均向右平移2个单位长度，得到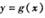的图象，求函数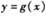的单调递减区间.

     

    查看答案和解析>>

    给出定义：若（其中为整数），则叫做离实数最近的整数，记作，在此基础上给出下列关于函数的四个命题：    

    ①函数=的定义域为，最大值是；②函数=在上是增函数；

    ③函数=是周期函数，最小正周期为1；④函数=的图象的对称中心是（0，0）.

    其中正确命题的序号是__________

    三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．)

    查看答案和解析>>

    本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
    （1）选修4-2：矩阵与变换
    已知矩阵M=
    01
    10
    ，N=
    0-1
    10

    （Ⅰ）求矩阵NN；
    （Ⅱ）若点P（0，1）在矩阵M对应的线性变换下得到点P′，求P′的坐标．
    （2）选修4-4：坐标系与参数方程
    在直角坐标系xOy中，直线l的参数方程是
    x=t
    y=2t+1
    （t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程是ρ=2cosθ（Ⅰ）在直角坐标系xOy中，求圆C的直角坐标方程
    （Ⅱ）求圆心C到直线l的距离．
    （3）选修4-5：不等式选讲
    已知函数f（x）=|x-1|
    （Ⅰ）解不等式f（x）＞2；
    （Ⅱ）求函数y=f（-x）+f（x+5）的最小值．

    查看答案和解析>>

    本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．
    （Ⅰ）选修4-2：矩阵与变换，
    已知矩阵A=
    01
    a0
    ，矩阵B=
    02
    b0
    ，直线l1    ：x-y+4=0经矩阵A所对应的变换得直线l2，直线l2又经矩阵B所对应的变换得到直线l3：x+y+4=0，求直线l2的方程．
    （Ⅱ）选修4-4：坐标系与参数方程，
    求直线
    x=-2+2t
    y=-2t
    被曲线
    x=1+4cosθ
    y=-1+4sinθ
    截得的弦长．
    （Ⅲ）选修4-5：不等式选讲，解不等式|x+1|+|2x-4|＞6．

    查看答案和解析>>

    本题（1）（2）（3）三个选答题，每小题5分，请考生任选1题作答，如果多做，则按所做的前1题计分．
    （1）（选修4-1，几何证明选讲）如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB=AD=a，CD=
    a
    2
    ，点E，F分别为线段AB，CD的中点，则EF=
    a
    2
    a
    2
    ．
    （2）（选修4-4，坐标系与参数方程）在极坐标系（ρ，θ）（0≤θ≤2π）中，曲线ρ=2sinθ与ρcosθ=-1的交点的极坐标为
    （
    		2
    ，
    3π
    4
    ）
    （
    		2
    ，
    3π
    4
    ）
    ．
    （3）（选修4-1，不等式选讲）已知函数f（x）=|x-a|．若不等式f（x）≤3的解集为{x|-1≤x≤5}，则实数a的值为
    a=2
    a=2
    ．

    查看答案和解析>>


    同步练习册答案