矩形仓库的多种设计方案

　　实践与探索课上，老师布置了这样一道题：

　　有100米长的篱笆材料，想围成一矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长50米的旧墙．有人用这个篱笆围一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求．现在请你设计矩形仓库的长和宽，使它符合要求．

　　经过同学们一天的实践与思考，老师收到了如下几种设计方案：

　　(1)如果设矩形的宽为x米，则用于长的篱笆为＝(50－x)米，这时面积S＝x(50－x)．

　　当S＝600时，由x(50－x)＝600，得x²－50x＋600＝0，解得x₁＝20，x₂＝30．

　　检验后知x＝20符合要求．

　　(2)根据在周长相等的条件下，正方形面积大于矩形面积，所以设计成正方形仓库，它的边长为x米，则4x＝100，x＝25．这时面积达到625米，当然符合要求．

　　(3)如果利用场地北面的那堵旧墙，取矩形的长与旧墙平行，设与墙垂直的矩形一边长为x米，则另一边为100－2x，如图．

　　因为旧墙长50米，所以100－2x≤50．即x≥25米．若S＝600平方米，则由x(100－2x)＝600，即x²－50x＋300＝0，解得x₁＝25＋，x₂＝25－．根据x≥25，舍去x₂＝25－．

　　所以，利用旧墙，取矩形垂直于旧墙一边长为25＋米(约43米)，另一边长约14米，符合要求．

　　(4)如果充分利用北面旧墙，即矩形一边是50米旧墙时，用100米篱笆围成矩形仓库，则矩形另一边长为25米，这时矩形面积为S＝50×25＝1250(平方米)．即面积可达1250平方米，符合设计要求．

还可以有其他一些符合要求的设计方案．请你试试看．

查看答案和解析>>

查看答案和解析>>

在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，作PE⊥AP，PE交射线DC于点E，射线AE交射线BC于点F，设BP=x，CE=y．
（1）如图，当点P在边BC上时（点P与点B、C都不重合），求y关于x的函数解析式，并写出它的定义域；
（2）当x=3时，求CF的长；
（3）当tan∠PAE=

1

2

时，求BP的长．

查看答案和解析>>

在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，作PE⊥AP，PE交射线DC于点E，射线AE交射线BC于点F，设BP=x，CE=y．
（1）如图，当点P在边BC上时（点P与点B、C都不重合），求y关于x的函数解析式，并写出它的定义域；
（2）当x=3时，求CF的长；
（3）当tan∠PAE=时，求BP的长．

查看答案和解析>>

在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，作PE⊥AP，PE交射线DC于点E，射线AE交射线BC于点F，设BP=x，CE=y．
（1）如图，当点P在边BC上时（点P与点B、C都不重合），求y关于x的函数解析式，并写出它的定义域；
（2）当x=3时，求CF的长；
（3）当tan∠PAE=时，求BP的长．

查看答案和解析>>

说明：若有本参考答案没有提及的解法，只要解答正确，请参照给分．

第I卷（选择题    共24分）

一、选择题（本大题共8题，每题3分，共24分）

1．B  2．C  3．C  4．B  5．D  6．C  7．A  8．B

第II卷（非选择题    共126分）

二、填空题：（每题3分，共30分）

9．；    10．；    11．；      12．；    13．抽样调查

14．范；    15．；    　　　16．60；     　　　17．；   18．8

说明：第11题若答案是不给分；第17题若答案是给2分．

三、解答题：（本大题共8题，共96分）

19．（1）解：原式

．

说明：第一步中每对一个运算给1分，第二步2分．

（2）解：原式

．

20．解：（1）15    5.5      6     1.8 ．

（2）①平均数或中位数或众数；

②平均数不能较好地反映乙队游客的年龄特征．

因为乙队游客年龄中含有两个极端值，受两个极端值的影响，导致乙队游客年龄方差较大，平均数高于大部分成员的年龄．

说明：第（1）题中平均数、中位数、众数各1分，方差2分，第（2）题中学生说理只要说出受“极端值影响”的大意即可给分．

21．解：（1）的数量关系是．

理由如下：．

又，

（SAS）．

．

（2）线段是线段和的比例中项．

理由如下：，．

．

又，

．

．

即线段是线段和的比例中项．

说明：若第（1）、（2）题中结论已证出，但在证明前未作判断的不扣分．

22．解：（1）不同意小明的说法．

因为摸出白球的概率是，摸出红球的概率是，

因此摸出白球和摸出红球不是等可能的．

（2）树状图如图（列表略）

（两个球都是白球）

（3）（法一）设应添加个红球，

由题意得

解得（经检验是原方程的解）

答：应添加3个红球．

（法二）添加后（摸出红球）

添加后（摸出白球）

添加后球的总个数．

应添加个红球．

23．解：（1）设该校采购了顶小帐篷，顶大帐篷．

根据题意，得

解这个方程组，得

（2）设甲型卡车安排了辆，则乙型卡车安排了辆．

根据题意，得

解这个不等式组，得．

车辆数为正整数，或16或17．

或4或3．

答：（1）该校采购了100顶小帐篷，200顶大帐篷．

（2）安排方案有：①甲型卡车15辆，乙型卡车5辆；②甲型卡车16辆，乙型卡车4辆；③甲型卡车17辆，乙型卡车3辆．

24．解：（1）所在直线与小圆相切，

理由如下：过圆心作，垂足为，

是小圆的切线，经过圆心，

，又平分．

．

所在直线是小圆的切线．

（2）

理由如下：连接．

切小圆于点，切小圆于点，

．

在与中，

，

（HL）   ．

，．

（3），．

，．

圆环的面积

又，  ．

说明：若第（1）、（2）题中结论已证出，但在证明前未作判断的不扣分．

25．解：（1）将和代入一次函数中，有．

  ．

经检验，其它点的坐标均适合以上解析式，

故所求函数解析式为．

（2）设前20天日销售利润为元，后20天日销售利润为元．

由，

，当时，有最大值578（元）．

由．

且对称轴为，函数在上随的增大而减小．

当时，有最大值为（元）．

，故第14天时，销售利润最大，为578元．

（3）

对称轴为．

，当即时，随的增大而增大．

又，．

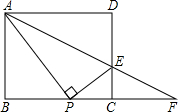
26．解：（1）在矩形中，，

，

．

．

（2）（法一），易得，．

．

梯形面积．

．

，．（负值舍去，经检验是原方程的解）

（法二）由（1）得．

，易得，．

，，

，

．（负值舍去，经检验是原方程的解）

（3）（法一）与（1）、（2）同理得，

．

直线过点．．

．（负值舍去，经检验是原方程的解）

（法二）连接交于点，则．

又，．

．是等边三角形，

．

（4）（法一）在中，，，，

由有：，．

，．

，又，．

，

与的函数关系式是，．

（法二）在中，．

由，有．

，，

，又．

，，

．

与的函数关系式是，．

说明：写出和各得1分．