
题目列表(包括答案和解析)
某商店老师设计了如下有奖游戏方案:顾客只要10元钱,即可参加有奖游戏一次。游戏规则如下:在图示的棋盘中,棋子从M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,则必须通过掷一次骰子(每个面分别标有1,2,3,4,5,6的正方体玩具)的方法来确定(否则,不必投骰子)——当出现“1”朝上时,沿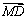 方向跳;当出现“2”,“4”,“6”朝上时,沿
方向跳;当出现“2”,“4”,“6”朝上时,沿 方向跳;当出现“3”, “5”朝上时,沿
方向跳;当出现“3”, “5”朝上时,沿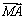 方向跳。奖励标准如下表:
方向跳。奖励标准如下表:
|
从M到N所用步数 |
2 |
3 |
4 |
|
奖金 |
100 |
10 |
5 |
若该商店平均每天有100人参加游戏,按每月30天计.
(1)写出每位顾客一次游戏后,该店获利的分布列;
(2)该店开展此项游戏每月大约获利多少元?(精确到1元)

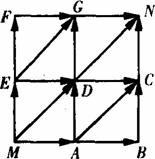
从M到N所用步数 | 2 | 3 | 4 |
奖金(元) | 100 | 10 | 5 |
若该店平均每天有100人次参加游戏,按每月30天计.
(Ⅰ)写出每位顾客一次游戏后,该店获利的分布列;
(Ⅱ)该店开展此项游戏每月大约获利多少元?(精确到1元)
 的概率分布;
的概率分布; .
.(理)2008年在中国北京成功举行了第29界奥运赛,其中乒乓球比赛实行五局三胜的规则,即先胜三局的获胜,比赛到此宣布结束。在赛前,有两个国家进行了友谊赛,比赛双方并没有全部投入主力,两队双方较强的队伍每局取胜的概率为0.6,若前四局出现2比2平局,较强队就更换主力,则其在决赛局中获胜的概率为0.7,设比赛结束时的局数为![]()
求![]() 的概率分布;
的概率分布;
求E![]() .
.
(本题满分16分)第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分6分。
 各项均为正数的数列
各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足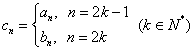 ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 为偶数时,求
为偶数时,求![]() ;
;
(3)若数列![]() ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的![]() ,试图确定
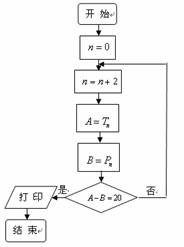
,试图确定![]() 的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
的值是否可以等于20?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com