
题目列表(包括答案和解析)
请先阅读:
设平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
当且仅当è=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)试求函数![]() 的最大值.
的最大值.
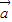 =(a1,a2),
=(a1,a2),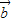 =(b1,b2),且
=(b1,b2),且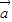 与
与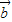 的夹角为θ,
的夹角为θ,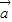 •
•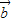 =|
=|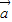 ||
||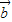 |cosθ,
|cosθ,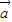 •
•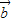 ≤|
≤|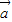 ||
||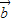 |.
|.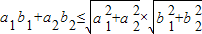 ,
,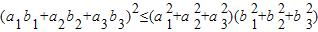 成立;
成立;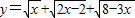 的最大值.
的最大值.已知函数 ,
,
(1)求函数 的定义域;
的定义域;
(2)求函数 在区间
在区间 上的最小值;
上的最小值;
(3)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 的定义域上的任意
的定义域上的任意 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】第一问中,利用由 即
即

第二问中, ,
, 得:
得:

 ,
,

第三问中,由在函数 的定义域上
的任意
的定义域上
的任意 ,
, ,当且仅当
,当且仅当 时等号成立。当命题p为真时,
时等号成立。当命题p为真时, ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由 即
即

(2) ,
, 得:
得:

 ,
,

(3)由在函数 的定义域上
的任意
的定义域上
的任意 ,
, ,当且仅当
,当且仅当 时等号成立。当命题p为真时,
时等号成立。当命题p为真时, ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,
当命题p为假,命题q为真时, ,
,
所以
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| b | 2 1 |
| b | 2 2 |
| b | 2 3 |
| x |
| 2x-2 |
| 8-3x |
某同学对函数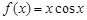 进行研究后,得出以下五个结论:①函数
进行研究后,得出以下五个结论:①函数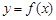 的图象是中心对称图形;②对任意实数
的图象是中心对称图形;②对任意实数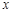 ,
,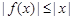 均成立;③函数
均成立;③函数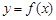 的图象与
的图象与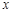 轴有无穷多个公共点,且任意相邻两点的距离相等;④函数
轴有无穷多个公共点,且任意相邻两点的距离相等;④函数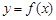 的图象与直线
的图象与直线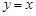 有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数
有无穷多个公共点,且任意相邻两点的距离相等;⑤当常数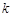 满足
满足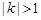 时,函数
时,函数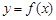 的图象与直线
的图象与直线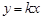 有且仅有一个公共点。其中所有正确结论的序号是 ( )
有且仅有一个公共点。其中所有正确结论的序号是 ( )
A.①②④ B.①②③④ C.①②④⑤ D.①②③④⑤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com