
题目列表(包括答案和解析)
(本小题满分14分)
已知数列![]() 满足:
满足:![]()
(I)求证:数列![]() 为等比数列;
为等比数列;
(II)求证:数列![]() 为递增数列;
为递增数列;
(III)若当且仅当![]() 的取值范围。
的取值范围。
(09年海淀区期末理)(14分)
如果正数数列![]() 满足:对任意的正数M,都存在正整数
满足:对任意的正数M,都存在正整数![]() 则称数列
则称数列![]() 是一个无界正数列。
是一个无界正数列。
(I)若 分别判断数列
分别判断数列![]() 、
、![]() 是否为无界正数列,并说明理由;
是否为无界正数列,并说明理由;
(II)若![]() 成立。
成立。
(III)若数列![]() 是单调递增的无界正数列,求证:存在正整数m,使得
是单调递增的无界正数列,求证:存在正整数m,使得
![]()
称满足以下两个条件的有穷数列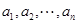 为
为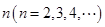 阶“期待数列”:
阶“期待数列”:
①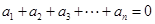 ;②
;②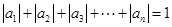 .
.
(1)若等比数列 为
为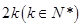 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是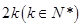 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列” 的前k项和为
的前k项和为 :
:
(i)求证: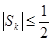 ;
;
(ii)若存在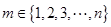 使
使 ,试问数列
,试问数列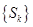 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”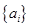 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
设集合W由满足下列两个条件的数列![]() 构成:
构成:
①![]()
②存在实数M,使![]() (n为正整数)
(n为正整数)
(I)在只有5项的有限数列![]()
![]() ;试判断数列
;试判断数列![]() 是否为集合W的元素;
是否为集合W的元素;
(II)设![]() 是各项为正的等比数列,
是各项为正的等比数列,![]() 是其前n项和,
是其前n项和,![]() 证明数列
证明数列![]() ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列![]() 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有![]() .
.
求证:数列![]() 单调递增.
单调递增.
一、选择题:
BDDCB BBAAC AC
二、填空题:
13. 14.6 15.
14.6 15. 16.
16.
|