阅读下面材料，按要求完成后面作业.

　　三角形内角平分线性质定理：三角形内角平分线分对边所得的两条线段和这个角的两边对应成比例.

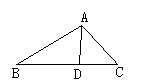
已知：△ABC中，AD是角平分线(如图).

求证：＝_.

　　分析：要证＝，一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似，现在B、D、C在一条直线，△ABD与△ADC不相似，需要考虑用别的方法换比.

在比例式＝中，AC恰好是BD、DC、AB的第四比例项，所以考虑过C作CE∥AD交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明＝，就可转化证＝_.

　　1.完成证明过程：

证明：

　　2.上述证明过程中，用到了哪些定理(写对两个即可)

　　答：用了:①

　　        ②

　　3.在上述分析和你的证明过程中，主要用到了下列三种数学思想的哪一种，①数形结合思想  ②转化思想  ③分类讨论思想

　　答：

　　4.用三角形内角平分线定理解答问题：

　　如图，△ABC中，AD是角平分线，AB＝5cm，AC＝4cm，BD＝7cm，求BD之长.

等腰△ABC，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转．

1.如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE～△CFP；

2.操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．

探究１：△BPE与△CFP还相似吗？（只需写出结论）(2分)

探究２：连结EF，△BPE与△PFE是否相似？请说明理由；

等腰△ABC，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转．
【小题1】如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE～△CFP；
【小题2】操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
探究１：△BPE与△CFP还相似吗？（只需写出结论）(2分)
探究２：连结EF，△BPE与△PFE是否相似？请说明理由；

等腰△ABC，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转．

1.如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE～△CFP；

2.操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．

探究１：△BPE与△CFP还相似吗？（只需写出结论）(2分)

探究２：连结EF，△BPE与△PFE是否相似？请说明理由；