
题目列表(包括答案和解析)
![]() (据荆州资料第58页第2题改编)在梯形ABCD中,AD∥BC,BA⊥AC,∠B = 450,AD = 2,BC = 6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上。
(据荆州资料第58页第2题改编)在梯形ABCD中,AD∥BC,BA⊥AC,∠B = 450,AD = 2,BC = 6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上。
(1) 求过A、D、C三点的抛物线的解析式。
(2) 求△ADC的外接圆的圆心M的坐标,并求⊙M的半径。
(3) E为抛物线对称轴上一点,F为y轴上一点,求当ED+EC+FD+FC最小时,EF的长。
(4) 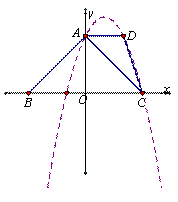 设Q为射线CB上任意一点,点P为对称轴左侧抛物线上任意一点,问是否存在这样的点P、Q,使得以P、Q、C为顶点的△与△ADC相似?若存在,直接写出点P、Q的坐标,若不存在,则说明理由。
设Q为射线CB上任意一点,点P为对称轴左侧抛物线上任意一点,问是否存在这样的点P、Q,使得以P、Q、C为顶点的△与△ADC相似?若存在,直接写出点P、Q的坐标,若不存在,则说明理由。
)如图,RtΔABC中,∠ACB=90°,AC=4,BA=5,点P是AC上的动点(P不与A、C重合)设PC=x,点P到AB的距离为y。
(1
)求y与x的函数关系式;(2
)试讨论以P为圆心,半径为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围。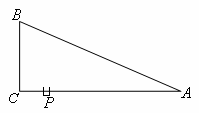
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com