
题目列表(包括答案和解析)
设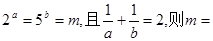 ( )
( )
A.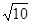 B.10 C.20 D.10
B.10 C.20 D.10
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.1 1 |
| 2 |
| π |
| 4 |
|
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
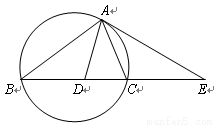
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:![]() 。
。

B.选修4—2 矩阵与变换
在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系![]() 中,点
中,点![]() 是椭圆
是椭圆![]() 上的一个动点,求
上的一个动点,求![]() 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:![]() 。
。
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。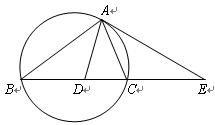 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 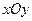 中,设椭圆 中,设椭圆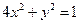 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 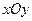 中,点 中,点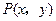 是椭圆 是椭圆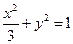 上的一个动点,求 上的一个动点,求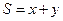 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
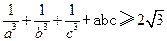 。
。从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证: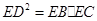 。
。
B.选修4—2 矩阵与变换
在平面直角坐标系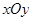 中,设椭圆
中,设椭圆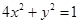 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系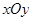 中,点
中,点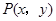 是椭圆
是椭圆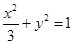 上的一个动点,求
上的一个动点,求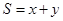 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证: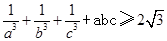 。
。
一、选择题:本大题共12小题,每小题5分,共60分.
1.B 2.C 3.【理】C 【文】B 4.A 5.C 6.D
7.C 8.C 9.【理】D 【文】B 10.A 11.B 12.【理】C 【文】D
二、填空题:本大题共4小题,每小题5分,共20分.
13. 2 14. -数学.files/image160.gif) 15.
15.-数学.files/image162.gif)
-数学.files/image164.gif) 16.
16. -数学.files/image166.gif)
三、解答题:本大题共6小题,共70分.
17.(本题满分10分)
解:-数学.files/image168.gif) .……….2分
.……….2分
(Ⅰ)-数学.files/image170.gif) 当
当-数学.files/image172.gif) ,
,
-数学.files/image176.gif)
-数学.files/image178.gif) .
………5分
.
………5分
(Ⅱ)【理】-数学.files/image180.gif)
-数学.files/image182.gif) ………7分
………7分
-数学.files/image184.gif)
-数学.files/image186.gif)
-数学.files/image188.gif) ,
,
-数学.files/image190.gif)
-数学.files/image192.gif) .
………10分
.
………10分
【文】-数学.files/image180.gif)
-数学.files/image182.gif) ………8分
………8分
-数学.files/image196.gif) .
………10分
.
………10分
18.(本题满分12分)
解:(Ⅰ)甲射击一次,未击中目标的概率为-数学.files/image198.gif) , ………2分
, ………2分
因此,甲射击两次,至少击中目标一次的概率为-数学.files/image200.gif) . ……...6分
. ……...6分
(Ⅱ)设“甲、乙两人各射击两次,甲击中目标2次,乙未击中”为事件-数学.files/image202.gif) ;“甲、乙两人各射击两次,乙击中目标2次,甲未击中”为事件
;“甲、乙两人各射击两次,乙击中目标2次,甲未击中”为事件-数学.files/image204.gif) ;“甲、乙两人各射击两次,甲、乙各击中1次”为事件
;“甲、乙两人各射击两次,甲、乙各击中1次”为事件-数学.files/image206.gif) ,
,
则
-数学.files/image208.gif) ;
………7分
;
………7分
-数学.files/image210.gif) ;
………8分
;
………8分
-数学.files/image212.gif) .
………9分
.
………9分
因为事件“甲、乙两人各射击两次,共击中目标2次”为-数学.files/image214.gif) ,而
,而-数学.files/image216.gif) 彼此互斥,
彼此互斥,
所以,甲、乙两人各射击两次,共击中目标2次的概率为
-数学.files/image218.gif) . ……….12
分
. ……….12
分
19.(本题满分12分))
【理科】解:(Ⅰ)
-数学.files/image220.gif)
-数学.files/image222.gif) 两式相减得
两式相减得
-数学.files/image224.gif) 从而
从而-数学.files/image226.gif) ,
………3分
,
………3分
-数学.files/image228.gif)
-数学.files/image230.gif) ,可知
,可知-数学.files/image232.gif) .
.-数学.files/image234.gif) .
.
-数学.files/image236.gif) 又
又-数学.files/image238.gif) .
.
-数学.files/image240.gif) 数列
数列-数学.files/image242.gif) 是公比为2,首项为4的等比数列, ………5分
是公比为2,首项为4的等比数列, ………5分
因此-数学.files/image244.gif) (
(-数学.files/image246.gif) )
………6分
)
………6分
(Ⅱ)据(Ⅰ)-数学.files/image248.gif)
-数学.files/image250.gif)
-数学.files/image252.gif)
-数学.files/image254.gif)
(当且仅当n=5时取等号). ………10分
-数学.files/image256.gif) 恒成立,
恒成立,-数学.files/image258.gif)
因此-数学.files/image260.gif) 的最小值是
的最小值是-数学.files/image262.gif) . ………12分
. ………12分
【文科】(Ⅰ)∵等差数列-数学.files/image264.gif) 中,公差
中,公差-数学.files/image266.gif) ,
,
∴-数学.files/image268.gif) ,
………3分
,
………3分
-数学.files/image270.gif)
-数学.files/image272.gif) ………6分
………6分
(Ⅱ)-数学.files/image274.gif) ,
………8分
,
………8分
令-数学.files/image276.gif) ,即得
,即得-数学.files/image278.gif) , ………10分
, ………10分
-数学.files/image280.gif) .
.
-数学.files/image282.jpg)
-数学.files/image240.gif) 数列
数列-数学.files/image285.gif) 为等差数列,∴存在一个非零常数
为等差数列,∴存在一个非零常数-数学.files/image276.gif) ,使
,使-数学.files/image286.gif) 也为等差数列. ………12分
也为等差数列. ………12分
20.(本题满分12分)
证明(Ⅰ)法1:取-数学.files/image288.gif) 中点
中点-数学.files/image290.gif) ,连接
,连接-数学.files/image292.gif) ,
,
∵-数学.files/image294.gif) 为
为-数学.files/image296.gif) 中点,
中点,
-数学.files/image240.gif)
-数学.files/image299.gif) 平行且等于
平行且等于-数学.files/image301.gif) ,
,
又∵E为BC的中点,四边形-数学.files/image303.gif) 为正方形,
为正方形,
-数学.files/image305.jpg) ∴
∴-数学.files/image307.gif) 平行且等于
平行且等于-数学.files/image301.gif) ,
,
∴四边形-数学.files/image309.gif) 为平行四边形,
………3分
为平行四边形,
………3分
∴-数学.files/image311.gif) ,又
,又-数学.files/image313.gif) 平面
平面-数学.files/image315.gif) ,
,-数学.files/image317.gif) 平面
平面-数学.files/image315.gif) ,
,
因此,-数学.files/image319.gif) 平面
平面-数学.files/image315.gif) .
………5分
.
………5分
法2:取AD的中点M,连接EM和FM,
∵F、E为PD和BC中点,
∴-数学.files/image321.gif) ,
,
∴平面-数学.files/image323.gif) , ………3分
, ………3分
-数学.files/image325.gif) 平面
平面-数学.files/image327.gif)
因此,-数学.files/image319.gif) 平面
平面-数学.files/image315.gif) .
………5分
.
………5分
解(Ⅱ)【理科】:连接-数学.files/image329.gif) ,连接
,连接-数学.files/image331.gif) 并延长,交
并延长,交-数学.files/image333.gif) 延长线于一点
延长线于一点-数学.files/image335.gif) ,
,
-数学.files/image337.gif) 连接
连接-数学.files/image339.gif) ,则
,则-数学.files/image339.gif) 为平面
为平面-数学.files/image341.gif) 和平面
和平面-数学.files/image343.gif) 的交线,
的交线,
作-数学.files/image345.gif) ,
………7分
,
………7分
∵-数学.files/image347.gif) 平面
平面-数学.files/image303.gif) ,∴
,∴-数学.files/image350.gif) ,
,
又∵-数学.files/image352.gif) ,
,
∴-数学.files/image354.gif) 平面
平面-数学.files/image356.gif) ,
,
则-数学.files/image358.gif) .
.
在等腰直角-数学.files/image360.gif) 中,
中,-数学.files/image362.gif) ,
,
-数学.files/image364.gif) 平面
平面-数学.files/image343.gif) ,
,
∴平面-数学.files/image367.gif) 平面
平面-数学.files/image343.gif) .
………10分
.
………10分
又平面-数学.files/image369.gif) 平面
平面-数学.files/image371.gif) .
.
∵-数学.files/image373.gif) 平面
平面-数学.files/image341.gif)
-数学.files/image376.gif) 平面
平面-数学.files/image343.gif) ,∴
,∴-数学.files/image379.gif) 为直线
为直线-数学.files/image381.gif) 与平面
与平面-数学.files/image343.gif) 所成的角.
所成的角.
设-数学.files/image384.gif) ,则
,则-数学.files/image386.gif) ,
,-数学.files/image388.gif) ,
,
在-数学.files/image390.gif) 中,
中,-数学.files/image392.gif) ,
,
∴-数学.files/image394.gif) .
.
因此,直线-数学.files/image381.gif) 与平面
与平面-数学.files/image343.gif) 所成的角
所成的角-数学.files/image396.gif) .….………………12分
.….………………12分
(Ⅱ)【文科】
承接法2,-数学.files/image398.gif) ,又
,又-数学.files/image400.gif) ,
,
∴-数学.files/image402.gif) ,
,
∵-数学.files/image347.gif) 平面
平面-数学.files/image303.gif) ,
,
∴平面-数学.files/image406.gif) 平面
平面-数学.files/image303.gif) .
………7 分
.
………7 分
-数学.files/image407.gif) ∴
∴-数学.files/image409.gif) 平面
平面-数学.files/image356.gif)
则-数学.files/image412.gif) 为直线
为直线-数学.files/image381.gif) 与平面
与平面-数学.files/image356.gif) 所成的角. ………9 分
所成的角. ………9 分
在-数学.files/image415.gif)
-数学.files/image327.gif) 中,
中,-数学.files/image418.gif) ,
,
∴-数学.files/image412.gif) =
=-数学.files/image421.gif) .
………12分
.
………12分
21.(本小题满分12分)
【理科】解:(I)设双曲线C的焦点为
-数学.files/image423.gif)
由已知-数学.files/image425.gif) ,
,
-数学.files/image427.gif) , ……………2分
, ……………2分
设双曲线-数学.files/image206.gif) 的渐近线方程为
的渐近线方程为-数学.files/image430.gif) ,
,
依题意,-数学.files/image432.gif) ,解得
,解得-数学.files/image434.gif) .
.
∴双曲线-数学.files/image206.gif) 的两条渐近线方程为
的两条渐近线方程为-数学.files/image437.gif) .
.
故双曲线-数学.files/image206.gif) 的实半轴长与虚半轴长相等,设为
的实半轴长与虚半轴长相等,设为-数学.files/image439.gif) ,则
,则-数学.files/image441.gif) ,得
,得-数学.files/image443.gif) ,
,
∴双曲线C的方程为-数学.files/image445.gif) ……………6分.
……………6分.
(II)由-数学.files/image447.gif) ,
,
直线与双曲线左支交于两点,
因此-数学.files/image449.gif) ………………..9分
………………..9分
又-数学.files/image451.gif) 中点为
中点为-数学.files/image453.gif)
∴直线-数学.files/image455.gif) 的方程为
的方程为-数学.files/image457.gif) ,
,
令x=0,得-数学.files/image459.gif) ,
,
∵-数学.files/image461.gif) ∴
∴-数学.files/image463.gif)
∴故-数学.files/image465.gif) 的取值范围是
的取值范围是-数学.files/image467.gif) . ………………12分.
. ………………12分.
【文科】解:(Ⅰ)-数学.files/image469.gif) 由已知
由已知-数学.files/image471.gif) 即
即-数学.files/image473.gif) 得
得-数学.files/image475.gif)
于是-数学.files/image477.gif) ……………..6分.
……………..6分.
(Ⅱ)-数学.files/image479.gif)
-数学.files/image481.gif)
-数学.files/image483.gif)
-数学.files/image485.gif)
-数学.files/image481.gif)
-数学.files/image487.gif)
-数学.files/image489.gif)
-数学.files/image479.gif) 恒成立,
恒成立,
-数学.files/image481.gif)
-数学.files/image489.gif)
-数学.files/image487.gif) 恒成立.
……………….8分.
恒成立.
……………….8分.
设-数学.files/image491.gif) ,则
,则-数学.files/image493.gif)
-数学.files/image495.gif) 上是增函数,在
上是增函数,在-数学.files/image497.gif) 上是减函数,
上是减函数,
从而-数学.files/image499.gif) 处取得极大值
处取得极大值-数学.files/image501.gif) 又
又-数学.files/image503.gif) 所以
所以-数学.files/image505.gif) 的最大值是6,故
的最大值是6,故-数学.files/image507.gif) .………………12分
.………………12分
22.(本小题满分12分)
【理科】解:(Ⅰ)-数学.files/image509.gif) 令
令-数学.files/image511.gif) 得
得-数学.files/image513.gif) ……………2分
……………2分
当-数学.files/image515.gif) 为增函数;
为增函数;
当-数学.files/image517.gif) 为减函数,
为减函数,
可知-数学.files/image060.gif) 有极大值为
有极大值为-数学.files/image520.gif) …………………………..4分
…………………………..4分
(Ⅱ)欲使-数学.files/image522.gif) 在
在-数学.files/image524.gif) 上恒成立,只需
上恒成立,只需-数学.files/image526.gif) 在
在-数学.files/image524.gif) 上恒成立,
上恒成立,
设-数学.files/image528.gif)
-数学.files/image530.gif) 由(Ⅰ)知,
由(Ⅰ)知,-数学.files/image532.gif) ,
,
-数学.files/image534.gif) ……………………8分
……………………8分
(Ⅲ)-数学.files/image536.gif) ,由上可知
,由上可知-数学.files/image538.gif) 在
在-数学.files/image540.gif) 上单调递增,
上单调递增,
-数学.files/image542.gif) ①,
①,
同理-数学.files/image544.gif) ②…………………………..10分
②…………………………..10分
两式相加得-数学.files/image546.gif)
-数学.files/image548.gif) ……………………………………12分
……………………………………12分
【文科】见理科21题答案.
[y1]Y cy
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com