
题目列表(包括答案和解析)
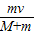
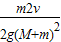
| A.从子弹射向木块到一起上升到最高点的过程中系统的机械能守恒 |
B.子弹射入木块瞬间动量守恒,故子弹射入木块瞬间子弹和木块的共同速度为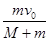 |
| C.忽略空气阻力,子弹和木块一起上升过程中系统机械能守恒,其机械能等于子弹射入木块前的动能 |
D.子弹和木块一起上升的最大高度为 |
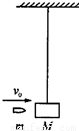
用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平射向木块,并停留在木块中,子弹初速度为v0,则下列判断正确的是
( )
A.从子弹射向木块到一起上升到最高点的过程中系统的机械能守恒
B.子弹射入木块瞬间动量守恒,故子弹射入木块瞬间子弹和木块的共同速度为
C.忽略空气阻力,子弹和木块一起上升过程中系统机械能守恒,其机械能等于子弹射入木块前的动能
D.子弹和木块一起上升的最大高度为、
【解析】:从子弹射向木块到一起运动到最高点的过程可以分为两个阶段:子弹射入木块的瞬间系统动量守恒,但机械能不守恒,有部分机械能转化为系统内能,之后子弹在木块中与木块一起上升,该过程只有重力做功,机械能守恒但总能量小于子弹射入木块前的动能,因此A、C错误;由子弹射入木块瞬间动量守恒可得子弹射入木块后的共同速度为,B正确;之后子弹和木块一起上升,该阶段机械能守恒可得上升的最大高度为,D正确.
用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图10所示.现有一质量为m的子弹自左方水平射向木块,并停留在木块中,子弹初速度为v0,则下列判断正确的是( )
| A.从子弹射向木块到一起上升到最高点的过程中系统的机械能守恒 |
B.子弹射入木块瞬间动量守恒,故子弹射入木块瞬间子弹和木块的共同速度为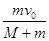 |
| C.忽略空气阻力,子弹和木块一起上升过程中系统机械能守恒,其机械能等于子弹射入木块前的动能 |
D.子弹和木块一起上升的最大高度为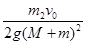 |
用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平射向木块,并停留在木块中,子弹初速度为v0,则下列判断正确的是
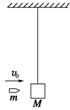
( )
A.从子弹射向木块到一起上升到最高点的过程中系统的机械能守恒
B.子弹射入木块瞬间动量守恒,故子弹射入木块瞬间子弹和木块的共同速度为
C.忽略空气阻力,子弹和木块一起上升过程中系统机械能守恒,其机械能等于子弹射入木块前的动能
D.子弹和木块一起上升的最大高度为、
【解析】:从子弹射向木块到一起运动到最高点的过程可以分为两个阶段:子弹射入木块的瞬间系统动量守恒,但机械能不守恒,有部分机械能转化为系统内能,之后子弹在木块中与木块一起上升,该过程只有重力做功,机械能守恒但总能量小于子弹射入木块前的动能,因此A、C错误;由子弹射入木块瞬间动量守恒可得子弹射入木块后的共同速度为,B正确;之后子弹和木块一起上升,该阶段机械能守恒可得上升的最大高度为,D正确.
一、二、选择题。
1. C 2. C 3. A 4. D 5. B 6. AB 7. ABD 8. AC 9. BD
三、简答题.本题共2小题,共计20分.把答案填在答题卡相应的横线上或按题目要求作答.
10.(1)7.2 (2分) 8.695(8.692~8.698均对) (2分)
(2) ①a.平衡摩擦力(1分) b.钩码的重力远小于小车的总重力(1分)
② (2分,其它正确也得分) 钩码的重力和小车的总质量 (2分)
(2分,其它正确也得分) 钩码的重力和小车的总质量 (2分)
11.(10分)
 (1)略(3分)
(1)略(3分)
(2)(3)
(3)(4分)(写出正确结果即给满分)
,电压表的电阻为RV,开关闭合电,电路中电流为I,外电路总电阻为
根据闭合电路欧姆定律有:E=U+Ir=U+ r,整理得:
r,整理得:
可见 图象为一条直线,故横坐标应表
图象为一条直线,故横坐标应表
直线的斜率为 由此解得:
由此解得:

四.简答题:本题有Ⅰ、Ⅱ、Ⅲ三组题,请在其中任选两组题作答;若三组题均答,则以Ⅰ、Ⅱ两组题计分,共24分,把答案填在题中的横线上或根据要求作答。
12.(1)BFH (全对得4分,不全对的,选对1个给1分,选错1个扣1分,扣完为止)
 (2)解:
(2)解:
①如图,紫光刚要发生全反射时的临界光线射在屏幕S上的点E到亮区中心G的距离r就是所求最半径。
设紫光临界角为C,由全反射的知识: (2分)
(2分)
由几何知识可知: 

 (1分)
(1分)
 (1分)
(1分)
 (1分)
(1分)

所以有: =
=
(其他几何关系解法,只要正确参考上述步骤给分)
②紫色。(2分)
13.(1) CDF (全对得4分,不全对的,选对1个给1分,选错1个扣1分,扣完为止)
(2) 解:(1)由质量数和电荷数守恒可知:
 (2分)
(2分)
(2)由题设条件可求出质量亏损为:
△m=2.0136u×2-(3.0150-1.0087)u=0.0035u
所以释放的核能为: (2分)
(2分)
(3)由动量和能量守恒有

解得: (1分)
(1分)
 (1分)
(1分)
14.(1)飞机水平速度不变  ① y方向加速度恒定
① y方向加速度恒定  ②
②
消去t即得  ③ 由牛顿第二定律
③ 由牛顿第二定律  ④
④
(2)在h处  ⑥
⑥  ⑦
⑦
①~④式 共4分 ⑥~⑦式 共4分(用动能定理或其他解法正确同样给分)
15、(12分) (1)证明:因为行星的质量M= (R是行星的半径),(1分)
(R是行星的半径),(1分)
行星的体积V=
 R3,所以行星的平均密度
R3,所以行星的平均密度 =
= =
= , (2分)
, (2分)
即 T2=
T2= ,是一个常量,对任何行星都相同。
(1分)
,是一个常量,对任何行星都相同。
(1分)
(2)空间探测器绕地球作圆周运动,有
由 =
= 得,空间站的轨道半径R=
得,空间站的轨道半径R= (1分)
(1分)
 =
=
随空间站一起运动时,空间探测器的动能为 mv2=
mv2= =
= (1分)
(1分)
随空间站一起运动时,空间探测器具有的机械能为
E1=- +
+ mv2=-
mv2=- =-
=- (2分)
(2分)
(3)空间站要脱离地球的引力,机械能最小值为E∞=0,因此,对探测器做功为
W=E∞-E1= (2分)
(2分)
由地面附近的重力加速度 得
得 2分)
2分)
16.
(1) (3分)
(3分)
在ab棒上升到最高点的过程中,根据能量守恒定律:
 (2分)
(2分)
Q=30J (1分) 电阻R上的热量:QR=Q/3=10J (1分)
(2)在0~T/4内,

 (1分)
(1分)
在T/4~T/2内,


 (2分)
(2分)
在3T/4~T内 Q3=Q1= (1分)
(1分)
 +
+ +
+ =5J (1分)解得:B0=0.5T (1分)
=5J (1分)解得:B0=0.5T (1分)
17.解:(1)粒子由a点进入磁场在洛仑兹力作用下做圆周运动,所以 ①(1分)
①(1分)
由题意知粒子圆周运动的半径: ② (1分)
② (1分)
 由①、②得:
由①、②得: (2分)
(2分)
(2)据题意,粒子在电场中的运动时间为周期的整数倍,
即: 于是得:
于是得: (1分)
(1分)
粒子在电场中运动侧向总位移: (2分)
(2分)
 带入已知量计算得:
带入已知量计算得: (1分)
(1分)
(3)由粒子在磁场中的受力可判断粒子带负电,粒子在 时刻进入电场后向N板偏转,由题意知粒子应刚好平行于N板从N板的边缘水平飞出.并沿着水平方向进入磁场.
时刻进入电场后向N板偏转,由题意知粒子应刚好平行于N板从N板的边缘水平飞出.并沿着水平方向进入磁场.
如图,设粒子从B点进入磁场,从C点射出,O"点为粒子圆周运动的圆心,由(1)知: ,所以OBO''C为菱形,故有
,所以OBO''C为菱形,故有 , (2分)
, (2分)
由于粒子水平射出,故O"B⊥v0,于是OC⊥v0,方向竖直,故aOC共线,
所以射出的点到a点的距为:aC=2R=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com