已知二次函数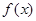的二次项系数为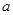，且不等式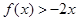的解集为,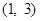

（1）若方程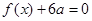有两个相等的根，求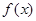的解析式；

（2）若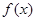的最大值为正数，求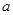的取值范围．

【解析】第一问中利用∵f(x)+2x>0的解集为(1,3),

设出二次函数的解析式，然后利用判别式得到a的值。

第二问中，

解：（1）∵f(x)+2x>0的解集为(1,3),

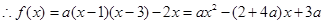   ①

由方程

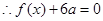
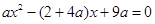              ②

∵方程②有两个相等的根，

∴，

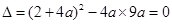即5a²-4a-1=0,解得a=1(舍) 或 a=-1/5

a=-1/5代入①得：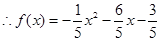

（2）由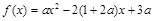

 

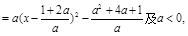
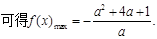
由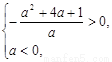 解得：

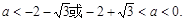
故当f(x)的最大值为正数时，实数a的取值范围是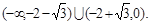

 

(本小题满分13分)

   某种家用电器每台的销售利润与该电器的无故障使用时间 (单位：年)有关. 若，则销售利润为元；若，则销售利润为元；若，则销售利润为元．设每台该种电器的无故障使用时间，及这三种情况发生的概率分别为，，，叉知，是方程的两个根，且   （1）求，，的值；  （2）记表示销售两台这种家用电器的销售利润总和，求的期望.

学科 (本小题满分12分)学网 某种家用电器每台的销售利润与该电器的无故障使用时间 (单位：年)有关. 若，则销售利润为元；若，则销售利润为元；若，则销售利润为元．设每台该种电器的无故障使用时间，及这三种情况发生的概率分别为，，，叉知，是方程的两个根，且学科网（1）求，，的值； （2）记表示销售两台这种家用电器的销售利润总和，求的期望.学科网

学科网

某种家用电器每台的销售利润与该电器的无故障使用时间T（单位：年）有关．若T≤1，则销售利润为0元；若1＜T≤3，则销售利润为100元；若T＞3，则销售利润为200元．设每台该种电器的无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率分别为P₁，P₂，P₃，又知P₁，P₂是方程25x₂-15x+a=0的两个根，且P₂=P₃．
（1）求P₁，P₂，P₃的值；
（2）记ξ表示销售两台这种家用电器的销售利润总和，求ξ的分布列；
（3）求销售两台这种家用电器的销售利润总和的平均值．