
题目列表(包括答案和解析)
“p或q”为真命题,“p且q为真命题”的
A.充分不必要条件 B.必要非充分条件
C.充要条件 D.即不充分也不必要条件
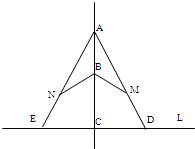 如图,森林的边界是直线L,兔子和狼分别在L的垂线AC上的点A和点B处(AB=BC=a),现兔子沿线AD(或AE)以速度2v准备越过L向森林逃跑,同时狼沿线段BM(点M在AD上)或BN(点N在AE上)以速度v进行追击,若狼比兔子先到或同时到达点M(或N)处,狼就会吃掉兔子.求
如图,森林的边界是直线L,兔子和狼分别在L的垂线AC上的点A和点B处(AB=BC=a),现兔子沿线AD(或AE)以速度2v准备越过L向森林逃跑,同时狼沿线段BM(点M在AD上)或BN(点N在AE上)以速度v进行追击,若狼比兔子先到或同时到达点M(或N)处,狼就会吃掉兔子.求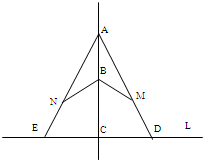 如图,森林的边界是直线L,兔子和狼分别在L的垂线AC上的点A和点B处(AB=BC=a),现兔子沿线AD(或AE)以速度2v准备越过L向森林逃跑,同时狼沿线段BM(点M在AD上)或BN(点N在AE上)以速度v进行追击,若狼比兔子先到或同时到达点M(或N)处,狼就会吃掉兔子.求兔子的所有不幸点(即可能被狼吃掉的地方)组成的区域的面积S.
如图,森林的边界是直线L,兔子和狼分别在L的垂线AC上的点A和点B处(AB=BC=a),现兔子沿线AD(或AE)以速度2v准备越过L向森林逃跑,同时狼沿线段BM(点M在AD上)或BN(点N在AE上)以速度v进行追击,若狼比兔子先到或同时到达点M(或N)处,狼就会吃掉兔子.求兔子的所有不幸点(即可能被狼吃掉的地方)组成的区域的面积S.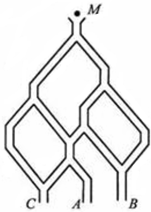 如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.
如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.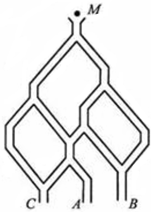 如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.
如图.一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C.则分别设为1,2,3等奖.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com