
题目列表(包括答案和解析)
| 2 |
| x |
| p |
| x |
| 1 |
| 16 |
| ||
| 2 |
| 1 |
| e |
| 1 |
| e |
 上存在两个不同点关于直线y=x对称,求出其坐标;若曲线
上存在两个不同点关于直线y=x对称,求出其坐标;若曲线 (p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的范围; 及
及 加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间
加以研究.当0<a<1时,就函数y=ax与y=logax的图象的交点情况提出你的问题,并加以解决.(说明:①函数f(x)=xlnx有如下性质:在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.) (p≠0)上存在两个不同点关于直线y=x对称,求实数p的取值范围;
(p≠0)上存在两个不同点关于直线y=x对称,求实数p的取值范围;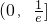 上单调递减,在区间
上单调递减,在区间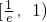 上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)
上单调递增.解题过程中可以利用;②将根据提出和解决问题的不同层次区别给分.)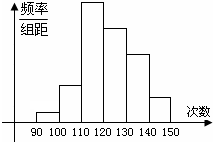 为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.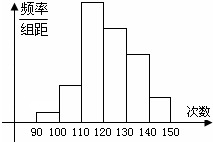 为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com