
题目列表(包括答案和解析)
本题有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵![]() 有特征值
有特征值![]() 及对应的一个特征向量
及对应的一个特征向量![]() .
.
(Ⅰ)求矩阵![]() ;
;
(Ⅱ)设曲线![]() 在矩阵
在矩阵![]() 的作用下得到的方程为
的作用下得到的方程为![]() ,求曲线
,求曲线![]() 的方程.
的方程.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若圆
为参数),若圆![]() 在以该直角坐标系的原点
在以该直角坐标系的原点![]() 为极点、
为极点、![]() 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
(3)(本小题满分7分)选修4—5:不等式选讲
已知函数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)记![]() 的最大值为
的最大值为![]() ,若正实数
,若正实数![]() 满足
满足![]() ,求
,求![]() 的最大值.
的最大值.
给出下列结论:
(1)在回归分析中,可用相关指数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好;
(2)某工产加工的某种钢管,内径与规定的内径尺寸之差是离散型随机变量;
(3)随机变量的方差和标准差都反映了随机变量的取值偏离于均值的平均程度,它们越小,则随机变量偏离于均值的平均程度越小;
(4)若关于 的不等式
的不等式 在
在 上恒成立,则
上恒成立,则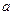 的最大值是1;
的最大值是1;
(5)甲、乙两人向同一目标同时射击一次,事件 :“甲、乙中至少一人击中目标”与事件
:“甲、乙中至少一人击中目标”与事件 :“甲,乙都没有击中目标”是相互独立事件。
:“甲,乙都没有击中目标”是相互独立事件。
其中结论正确的是 。(把所有正确结论的序号填上)
(1)用x0、f(x0)、f′(x0)表示m;
(2)证明当x0∈(0,+∞)时,g(x)≥f(x);
(3)若关于x的不等式x2+1≥ax+b≥![]() 在
在![]() 上恒成立,其中a、b为实数,求b的取值范围及a与b 所满足的关系.
上恒成立,其中a、b为实数,求b的取值范围及a与b 所满足的关系.
给出定义:若函数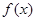 在
在 上可导,即
上可导,即 存在,且导函数
存在,且导函数 在
在 上也可导,则称
上也可导,则称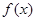 在
在 上存在二阶导函数,记
上存在二阶导函数,记 ,若
,若 在
在 上恒成立,则称
上恒成立,则称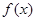 在
在 上为凸函数.以下四个函数在
上为凸函数.以下四个函数在 上不是凸函数的是(
)
上不是凸函数的是(
)
A. B.
B. C.
C. D.
D.
(05年辽宁卷)(12分)
函数![]() 在区间
在区间![]() 内可导,导函数
内可导,导函数![]() 是减函数,且
是减函数,且![]() .设
.设![]() ,
,![]() 是曲线
是曲线![]() 在点
在点![]() 处的切线方程,并设函数
处的切线方程,并设函数![]() .
.
(Ⅰ)用![]() 、
、![]() 、
、![]() 表示m;
表示m;
(Ⅱ)证明:当![]() ,
,![]() ;
;
(Ⅲ)若关于x的不等式![]() 在
在![]() 上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
上恒成立,其中a、b为实数,求b的取值范围及a与b所满足的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com