
题目列表(包括答案和解析)
已知命题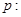 “椭圆
“椭圆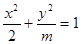 的焦点在
的焦点在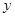 轴上”;
轴上”;
命题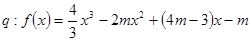 在
在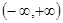 上单调递增,若“
上单调递增,若“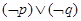 ”为假,求
”为假,求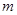 的取值范围.
的取值范围.
【解析】主要考查了命题中复合命题的真值问题的判定,以及椭圆,导数的运用。
首先求解若p为真,则m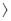 2.
2.
若q为真,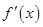 =
=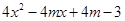
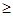 0在R上恒成立。
0在R上恒成立。
所以 
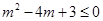 所以
所以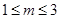
而要是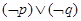 为假,则
为假,则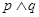 ,这样就可以得到了。
,这样就可以得到了。
若p为真,则m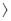 2.
2分
2.
2分
若q为真,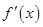 =
=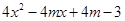
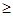 0在R上恒成立。
0在R上恒成立。
所以 
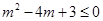 所以
所以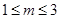 3分
3分
若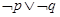 为假,所以
为假,所以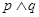 为真 2分
为真 2分
所以m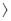 2且
2且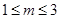 , 所以
, 所以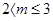
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为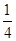 ,不堵车的概率为
,不堵车的概率为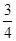 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为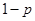 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为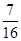 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得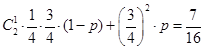
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 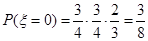 ,
, 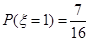
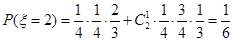 ,
,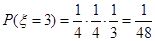
从而得到分布列和期望值
解:(I)由已知条件得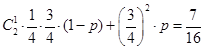 ,即
,即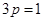 ,则
,则 的值为
的值为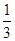 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 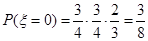 ,
, 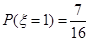
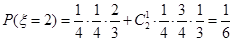 ,
,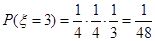
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以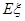
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com