
题目列表(包括答案和解析)
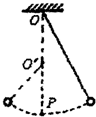 如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方O′处有一光滑的钉子,将小球从右侧某高度处无初速释放,当小球向左摆动通过最低点P时,细线将被钉子拦住,在此瞬间( )
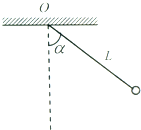
如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方O′处有一光滑的钉子,将小球从右侧某高度处无初速释放,当小球向左摆动通过最低点P时,细线将被钉子拦住,在此瞬间( )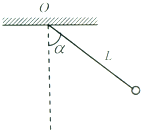 如图所示,质量为m的小球,用长为L的细线悬挂在水平天花板上的O点.现将小球偏离平衡位置,使细线与竖直方向的夹角为α,然后将小球由静止释放.当小球运动到最低点时,试求:
如图所示,质量为m的小球,用长为L的细线悬挂在水平天花板上的O点.现将小球偏离平衡位置,使细线与竖直方向的夹角为α,然后将小球由静止释放.当小球运动到最低点时,试求:如图所示,质量为m的小球,用长为l的不可伸长的细线挂在O点,在O点正下方![]() 处有一光滑的钉子O′。把小球拉到与钉子O′在同一水平高度的位置,摆线被钉子拦住且张紧,现将小球由静止释放,当小球第一次通过最低点P时( )
处有一光滑的钉子O′。把小球拉到与钉子O′在同一水平高度的位置,摆线被钉子拦住且张紧,现将小球由静止释放,当小球第一次通过最低点P时( )
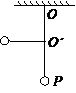
A.小球的运动速度突然减小
B.小球的角速度突然减小
C.小球的向心加速度突然减小
D.悬线的拉力突然减小

1. D 2. A 3. B 4. B 5. C 6. CD 7. AC 8. BD 9. ACD
11. 1.0 3.1×10-3
12. (1) 右侧 ① 变大 ② 变小 ③ 变小(2) dㄊ、sㄋ、εㄋ时,c变小 (3) A
13. (1)[ Fcosθ-μ(mg-Fsinθ)t1]/m=μgt2 ∴F=μmg(t2/t1+1)/(cosθ+μsinθ)=600/11 N
(2) x=1/2?μgt22+1/2?μgt2?t1=
 14. (1)
G?Mm/r2=mrω
14. (1)
G?Mm/r2=mrω
 (2)
Δt=2π/(ω-ω0)= 2π/√g/8R -ω0
(2)
Δt=2π/(ω-ω0)= 2π/√g/8R -ω0
15. (1) E=12V 12=6+6×r /2?r=2Ω
(2) Um=0, UM=[R /(R+r)]? E =11V
(3) R并=E/Im-r=4Ω 1/R+1/Rx=1/R并∴Rx=44/9Ω
 16. (1)
mv20/2=qU2 ∴v0=√2qU2/m
16. (1)
mv20/2=qU2 ∴v0=√2qU2/m
 (2)
1/2?qV1/md?(T/4)2×2≤d/2 ∴d≥√qU1T2/
(2)
1/2?qV1/md?(T/4)2×2≤d/2 ∴d≥√qU1T2/
 (3)
d2=1/2?qU2/md2?(T/4×n)2 ∴d2=n√qU2T2/
(3)
d2=1/2?qU2/md2?(T/4×n)2 ∴d2=n√qU2T2/
17. (1) 2R=gt2/
(2) mg=mv
(3) Fl=mg?2R+mv
当2mgR/l=mgl/8R,即l=4R时,有:Fm=mg.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com