
题目列表(包括答案和解析)
(本小题14分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时, 可全部租
出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月
需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?
最大月收益是多少?
(本小题14分)
某化工厂生产某种产品,每件产品的生产成本是3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11-x)2万件;若该企业所生产的产品全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数k (1≤k≤3)。
(1)求该企业正常生产一年的利润F(x)与出厂价x的函数关系式;
(2)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
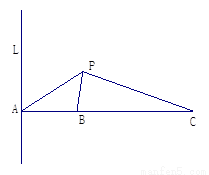
(1)设A到P的距离为 km,用
km,用 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)
(本小题12分)
已知某商品的价格 (元)与需求量
(元)与需求量 (件)之间的关系有如下一组数据:
(件)之间的关系有如下一组数据:
|
|
14 |
16 |
18 |
20 |
22 |
|
|
12 |
10 |
7 |
5 |
3 |
(1)画出 关于
关于 的散点图
的散点图
(2)用最小二乘法求出回归直线方程
(3)计算 的值,并说明回归模型拟合程度的好坏。
的值,并说明回归模型拟合程度的好坏。
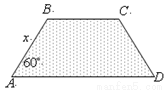
(本小题满分14分)某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为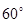 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为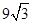 平方米,且高度不低于
平方米,且高度不低于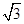 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为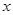 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为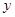 (米).
(米).
⑴求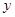 关于
关于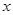 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过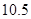 米,则其腰长
米,则其腰长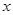 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长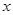 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com