(2006?静安区模拟)17世纪英国物理学家胡克发现:在弹性限度内,弹簧的形变量与弹力成正比,这就是著名的胡克定律.受此启发,一组同学研究“金属线材伸长量与拉力的关系”的探究过程如下:
A.有同学认为:横截面为圆形的金属丝或金属杆在弹性限度内,其伸长量与拉力成正比,与截面半径成反比.
B.他们准备选用一些“由同种材料制成的不同长度、不同半径的线材”作为研究对象,用测距仪、传感器等仪器测量线材的伸长量随拉力变化的规律,以验证假设.
C.通过实验取得如下数据:
| 长度 |
拉力伸长直径 |
250N |
500N |
750N |
1000N |
| 1m |
2.52mm |
0.4mm |
0.8mm |
1.2mm |
1.6mm |
| 2m |
2.52mm |
0.8mm |
1.6mm |
2.4mm |
3.2mm |
| 1m |
3.57mm |
0.2mm |
0.4mm |
0.6mm |
0.8mm |
D.同学们对实验数据进行分析、归纳后,对他们的假设进行了补充完善.
(1)上述科学探究活动中,属于“制定计划”和“搜集证据”的环节分别是
B
B
、
C
C
.
(2)请根据上述过程分析他们的假设是否全部正确?若有错误或不足,请给予修正.
在弹性限度内,金属丝的伸长量与拉力成正比,与截面半径的平方成反比,还与金属丝的长度成正比.
在弹性限度内,金属丝的伸长量与拉力成正比,与截面半径的平方成反比,还与金属丝的长度成正比.
.
在弹性限度内,金属丝的伸长量与拉力成正比,与截面半径的平方成反比,还与金属丝的长度成正比.
在弹性限度内,金属丝的伸长量与拉力成正比,与截面半径的平方成反比,还与金属丝的长度成正比.
.
(3)求出这种线材的伸长量与拉力以及材料的长度、截面积之间的定量关系式.
(4)有一工程要使用一根能承受98000N拉力的线材,按设计要求,其受拉力后的伸长不能超过原来长度的1/1000.现有一根用这种材料制成的金属杆,长为4m,横截面积为0.8cm
2,请通过计算说明能否使用这根金属杆.

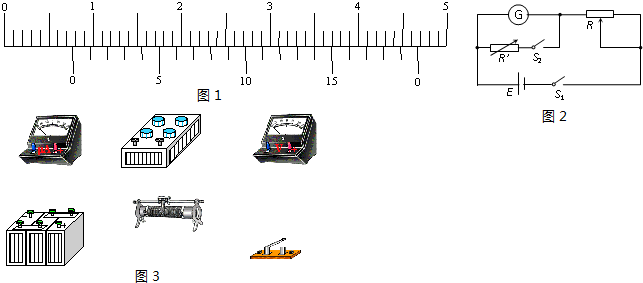
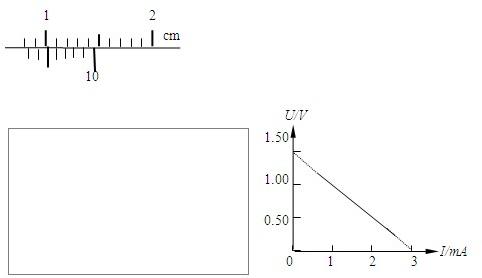
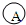 :满偏电流3mA,电阻约10Ω
:满偏电流3mA,电阻约10Ω :量程0-1.5V,电阻约1000Ω
:量程0-1.5V,电阻约1000Ω