
题目列表(包括答案和解析)
(本小题满分12分)设函数![]() .
.
(Ⅰ)求函数f (x)在点(0, f (0))处的切线方程;
(Ⅱ)求f (x)的极小值;
(Ⅲ)若对所有的![]() ,都有
,都有![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(本小题满分12分)
设函数f(x)=lnx,g(x)=ax+![]() ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值;
(Ⅱ) 设x>0,试比较f(x)与g(x)的大小.
(本小题满分12分)
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值;
(Ⅱ) 设x>0,试比较f(x)与g(x)的大小.
(本小题满分12分)
设函数f (x)=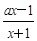 ,其中a∈R.
,其中a∈R.
(1)若a=1,f (x)的定义域为[0,3],求f (x)的最大值和最小值.
(2)若函数f (x)的定义域为区间(0,+∞),求a的取值范围使f (x)在定义域内是单调减函数.
(本小题满分12分)
设二次函数f(x)=ax2+bx(a≠0)满足条件:
①f(-1+x)=f(-1-x);②函数f(x)的图象与直线y=x只有一个公共点.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若不等式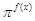 >(
>(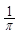 )2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
)2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
C
C
A
C
B
B
二、填空题
13..files/image229.gif) 14.
14. .files/image231.gif) 15.
15. .files/image233.gif) 16.___-1__
16.___-1__
三、解答题
17.解:1) .files/image235.gif)
=.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
2).files/image247.gif)
.files/image249.gif) 或
或.files/image251.gif)
.files/image253.gif) 或
或.files/image255.gif) ,而
,而.files/image257.gif)
.files/image259.gif)
.files/image261.gif) ,
,.files/image263.gif)
18.解:(I)由题意:.files/image265.gif) 的取值为1,3,又
的取值为1,3,又.files/image267.gif)
.files/image269.gif)
|