
题目列表(包括答案和解析)
 如图所示,在真空室内x轴正半轴M(
如图所示,在真空室内x轴正半轴M(3
| ||
| 10 |
在一真空室内存在着匀强电场和匀强磁场,电场的方向与磁场的方向相同,已知电场强度E=40.0V/m,磁感应强度B=0.30T,如图所示,在真空室内建立O—xyz三维直角坐标系,其中z轴竖直向上。质量m=1.0×10-4Kg、带负电的质点以速度v0=100m/s沿+x方向做匀速直线运动,速度方向与电场、磁场方向垂直,取g=10m/s2。
(1)求质点所受电场力与洛伦兹力的大小之比
(2)求带电质点的电荷量
(3)若在质点通过O点时撤去磁场,求经过t=0.20s时,带电质点的位置坐标。
在一真空室内存在着匀强电场和匀强磁场,电场的方向与磁场的方向相同,已知电场强度E=40.0V/m,磁感应强度B=0.30T,如图所示,在真空室内建立O—xyz三维直角坐标系,其中z轴竖直向上。质量m=1.0×10-4Kg、带负电的质点以速度v0=100m/s沿+x方向做匀速直线运动,速度方向与电场、磁场方向垂直,取g=10m/s2。

(1)求质点所受电场力与洛伦兹力的大小之比
(2)求带电质点的电荷量
(3)若在质点通过O点时撤去磁场,求经过t=0.20s时,带电质点的位置坐标。
如图所示,某一真空室内充满竖直向下的匀强电场E,在竖直平面内建立坐标xOy,在y<0的空间里有与场强E垂直的匀强磁场B,在y>0的空间内,将一质量为m的带电液滴(可视为质点)自由释放,此液滴则沿y轴的负方向,以加速度a=2g(g为重力加速度)做匀加速直线运动,当液滴运动到坐标原点时,瞬间被安置在原点的一个装置改变了带电性质(液滴所带电荷量和质量均不变),随后液滴进入y<0的空间运动.液滴在y<0的空间内的运动过程中( )

A.重力势能一定不断减小
B.电势能一定先减小后增大
C.动能不断增大
D.动能保持不变
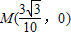 点固定一负的点电荷,电量Q=-6.4×10-6C.点电荷左侧的电场分布以y轴为界限.在x轴负半轴远离原点某处有一粒子放射源不断沿x轴正向放射出速度相同的带正电的粒子.粒子质量m=3.0×10-27kg,电量q=+3.2×10-19C,速率v=3.2×106m/s.为使带电粒子进入y轴右侧后作匀速圆周运动,最终打在位于x正半轴点电荷右侧的荧光屏上(未画出),可在y轴左侧加一个方向垂直纸面向外、圆心在x轴上的圆形匀强磁场区域,其磁感应强度B=0.30T.不计粒子重力,静电力常数K=9×109N?m2/C2.求:
点固定一负的点电荷,电量Q=-6.4×10-6C.点电荷左侧的电场分布以y轴为界限.在x轴负半轴远离原点某处有一粒子放射源不断沿x轴正向放射出速度相同的带正电的粒子.粒子质量m=3.0×10-27kg,电量q=+3.2×10-19C,速率v=3.2×106m/s.为使带电粒子进入y轴右侧后作匀速圆周运动,最终打在位于x正半轴点电荷右侧的荧光屏上(未画出),可在y轴左侧加一个方向垂直纸面向外、圆心在x轴上的圆形匀强磁场区域,其磁感应强度B=0.30T.不计粒子重力,静电力常数K=9×109N?m2/C2.求: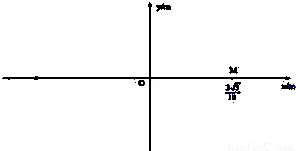
一、1、B 2、CD 3、BC 4、B 5、AD 6、B 7、B 8、BD
二、实验题:(18分)将答案填在题目的空白处,或者要画图连线。
9、(6分)(1)104.05 0.520 200(6分)
10、(12分)①见下图(5分)

②Ⅰ. 毫伏表的读数U,电流表的读数I(2分)
Ⅱ. 定值电阻R3的阻值(或定值电阻R2、R3的阻值)(2分)
③ (A电路)或
(A电路)或 (B电路)(3分)
(B电路)(3分)
三、本大题共三小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
11、(16分)(1)小车与墙壁碰撞后向左运动,木块与小车间发生相对运动将弹簧压缩至最短时,二者速度相等,此时弹簧的弹性势能最大,此过程中,二者组成的系统动量守恒,设弹簧压缩至最短时,小车和木块的速度大小为v,根据动量守恒定律有
m1v1-m2v0=(m1+m2)v ①(2分)
解得 v=
设最大的弹性势能为EP,根据机械能守恒定律可得
EP= m1v12+
m1v12+ m2v02-
m2v02- (m1+m2)v2
③ (2分)
(m1+m2)v2
③ (2分)
由②③得EP=3.6J ④(2分)
(2)根据题意,木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’ 时,木块将不会从小车上滑落, 此过程中,二者组成的系统动量守恒,故有v’ =v==
木块在A点右侧运动过程中,系统的机械能守恒,而在A点左侧相对滑动过程中将克服摩擦阻力做功,设此过程中滑行的最大相对位移为L,根据功能关系有
μm2gL=
 m1v12+
m1v12+ m2v02-
m2v02- (m1+m2)v’2
⑥(3分)
(m1+m2)v’2
⑥(3分)
解得L=
即车面A点左侧粗糙部分的长度应大于0.90m(2分)
12、(18分)(1) 对D到M到A到P过程,由能量守恒得: ……………①(2分)
……………①(2分)
由已知得:  ……………②(2分)
……………②(2分)
解①②得:x0=4R ……………………③(2分)
(2)
对D到M到A的过程由动能定理: ………④(2分)
………④(2分)
对A点由牛顿定律:
 ……………⑤(2分)
……………⑤(2分)
 …………… ⑥(2分)
…………… ⑥(2分)
3)由于5R>X0能到达P点,由动能定理
由动能定理 …………⑦(2分)
…………⑦(2分)
从P点到滑行停止
 ……………⑧(2分)
……………⑧(2分)
摩擦生热
 ……………………….…⑨(1分)
……………………….…⑨(1分)
解⑦⑧⑨得
 ………………….………⑩(2分)
………………….………⑩(2分)
13、(20分)(1)金属框开始运动时速度为零
感应电动势E=BLv1
回路中的电流
金属框受到的安培力
加速度大小 ,方向向右 (6分)
,方向向右 (6分)
(2)当金属框受到的阻力等于安培力时,金属框以恒定速度v2匀速运动
感应电动势E=BL(v1-v2)
回路中的电流
金属框受到的安培力
达到恒定速度v2时,受力平衡
解得 (8分)
(8分)
(3)系统消耗磁场能的功率,包括金属框发热功率和克服阻力的功率。即
 (3分)
(3分)
解得  (3分)
(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com