
题目列表(包括答案和解析)
 A.若关于x的不等式|x+1|+|x-3|≥a恒成立,则实数a的取值范围是
A.若关于x的不等式|x+1|+|x-3|≥a恒成立,则实数a的取值范围是| 3 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为| 1 |
| 3 |
| 1 |
| 3 |
| 7 |
| 7 |
|
| 3 |
| 3 |
.若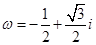 ,则等于
,则等于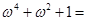 ( )
( )
A.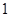 B.
B.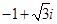 C.
C.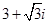 D.
D.

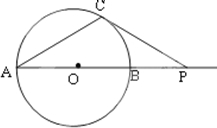
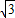 ,若∠CAP=30°,则⊙O的直径AB= .
,若∠CAP=30°,则⊙O的直径AB= .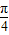 )=
)=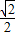 ,则极点到这条直线的距离是 .
,则极点到这条直线的距离是 .
 ,若∠CAP=30°,则⊙O的直径AB= .
,若∠CAP=30°,则⊙O的直径AB= .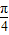 )=
)= ,则极点到这条直线的距离是 .
,则极点到这条直线的距离是 .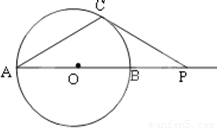
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.B 2.A 3.B 4.B 5.C 6.D 7.D 8.C 9.B 10.A 11.D 12.A
二、填空题(本大题共4小题,每小题4分,共16分)
13. 14.
14. 15.
15. 16.
16.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.解:(Ⅰ)
= …………………………………………………3分
…………………………………………………3分
 函数
函数 的周期
的周期 ,
,
由题意可知 ………………………………………6分
………………………………………6分
(Ⅱ)由(Ⅰ)可知
而 ………………………………………8分
………………………………………8分
由余弦定理知
 又
又 ,
,
 …………………………………………………………………12分
…………………………………………………………………12分
18.证明:(Ⅰ)
 面
面 面
面
 面
面 …………………………………………………………………………4分
…………………………………………………………………………4分
(Ⅱ) 面
面 面
面
 平面
平面 平面
平面 …………………………………………8分
…………………………………………8分
(Ⅲ)连接BE,易证明 ,由(2)知
,由(2)知 面
面
 平面
平面 ………………………………………………………………………12分
………………………………………………………………………12分
19.解:(Ⅰ)设抽到相邻两个月的数据为事件A.因为从6组数据中选取2组数据共有15种情况,每种情况都是等可能出现的.其中抽到相邻两个月的数据的情况有5种,所以
P(A)= ………………………………………………………………………………4分
………………………………………………………………………………4分
(Ⅱ)由数据求得 由公式求得
由公式求得
再由 ,得
,得 所以y关于x的线性回归方程为
所以y关于x的线性回归方程为 ………8分
………8分
(Ⅲ)当 时,
时,
同样,当 时,
时,
所以,该小组所得线性回归方程是理想的………………………………………………12分
20.(Ⅰ) 由题意得
由题意得 ,解得
,解得 ………………………2分
………………………2分
所以 令
令 则
则

 在
在 上单调递减,在
上单调递减,在 上单调递增,在
上单调递增,在 上单调递减……6分
上单调递减……6分
(Ⅱ)因存在 使得不等式
使得不等式 成立
成立
故只需要 的最大值
的最大值 即可
即可

①
若 ,则当
,则当 时,
时, 在
在 单调递增
单调递增
 当
当 时,
时,
 当
当 时,不存在
时,不存在 使得不等式
使得不等式 成立…………………………9分
成立…………………………9分
②
当 时,
时, 随x的变化情况如下表:
随x的变化情况如下表:
x




+
0
-

ㄊ

ㄋ
 当
当 时,
时, 由
由 得
得
综上得 ,即a的取值范围是
,即a的取值范围是 …………………………………………………12分
…………………………………………………12分
解法二:根据题意,只需要不等式 在
在 上有解即可,即
上有解即可,即 在
在 上有解,即不等式
上有解,即不等式 在
在 上有解即可……………………………9分
上有解即可……………………………9分
令 ,只需要
,只需要 ,而
,而
故 ,即a的取值范围是
,即a的取值范围是 ………………………………………………………12分
………………………………………………………12分
21.因 ①
①
 时
时 ②
②
由①-②得 ………………………………4分
………………………………4分
又 得
得 ,故数列
,故数列 是首项为1,公比
是首项为1,公比 的等比数列
的等比数列
 ………………………………………………………………………6分
………………………………………………………………………6分
(Ⅱ)假设满足题设条件的实数k,则 ………8分
………8分
由题意知,对任意正整数n恒有 又数列
又数列 单调递增
单调递增
所以,当 时数列中的最小项为
时数列中的最小项为 ,则必有
,则必有 ,则实数k最大值为1…………12分
,则实数k最大值为1…………12分
 22.解:(Ⅰ)由椭圆的方程知
22.解:(Ⅰ)由椭圆的方程知 点
点
设F的坐标为
 是⊙M的直径,
是⊙M的直径,


得 椭圆的离心率
椭圆的离心率 …………………………………………6分
…………………………………………6分
(Ⅱ) ⊙M过点F,B,C三点,
⊙M过点F,B,C三点, 圆心M既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为
圆心M既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为 ①
①
 BC的中点为
BC的中点为
 BC的垂直平分线方程为
BC的垂直平分线方程为 ②
②
由①②得 ,
, 即
即
 在直线
在直线 上,
上,
 由
由 得
得
 椭圆的方程为
椭圆的方程为 …………………………………………………………14分
…………………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com