
题目列表(包括答案和解析)






 的方程;
的方程; 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 和抛物线
和抛物线 的方程;
的方程; 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值. 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于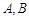 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,求
能否垂直?若能,求 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 之间满足的关系式.
之间满足的关系式.
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
答案
C
A
B
A
B
C
C
D
二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.
9..files/image207.gif) 10.
10..files/image209.gif) 11.
11..files/image211.gif) 12.
12. .files/image213.gif)
13. .files/image215.gif) 14.
14..files/image217.gif) 15.2
15.2
说明:第14题答案可以有多种形式,如可答.files/image219.gif) 或
或.files/image221.gif) Z
Z.files/image115.gif) 等, 均给满分.
等, 均给满分.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
解:(1)∵.files/image224.gif)
.files/image226.gif) …… 2分
…… 2分
.files/image228.gif) …… 4分
…… 4分
.files/image230.gif) .
…… 6分
.
…… 6分
∴.files/image232.gif) .
…… 8分
.
…… 8分
(2) 当.files/image234.gif) 时,
时, .files/image117.gif) 取得最大值, 其值为2 .
……10分
取得最大值, 其值为2 .
……10分
此时.files/image237.gif) ,即
,即.files/image239.gif)
.files/image241.gif) Z
Z.files/image115.gif) .
……12分
.
……12分
17.(本小题满分12分)
解:(1)设“这箱产品被用户接收”为事件.files/image060.gif) ,
,.files/image245.gif) . ……3分
. ……3分
即这箱产品被用户接收的概率为.files/image247.gif) .
……4分
.
……4分
(2).files/image121.gif) 的可能取值为1,2,3.
……5分
的可能取值为1,2,3.
……5分
.files/image250.gif) =
=.files/image252.gif) ,
,
.files/image254.gif) =
=.files/image256.gif) ,
,
.files/image258.gif) =
=.files/image260.gif) ,
……8分
,
……8分
∴.files/image121.gif) 的概率分布列为:
的概率分布列为:
.files/image121.gif)
1
2
3
……10分
.files/image104.gif)
.files/image265.gif)
.files/image267.gif)
.files/image269.gif)
∴.files/image271.gif) =
=.files/image273.gif) .
……12分
.
……12分
18.(本小题满分14分)
解:(1)∵点A、D分别是.files/image129.gif) 、
、.files/image131.gif) 的中点,
的中点,
∴.files/image275.gif) .
…… 2分
.
…… 2分
∴∠.files/image277.gif) =90º.
=90º.
∴.files/image279.gif) .
.
∴ .files/image281.gif) ,
,
∵.files/image283.gif) ,
,
∴.files/image154.gif) ⊥平面
⊥平面.files/image286.gif) . …… 4分
. …… 4分
∵.files/image288.gif) 平面
平面.files/image286.gif) ,
,
∴.files/image291.gif) .
…… 6分
.
…… 6分
(2)法1:取.files/image293.gif) 的中点
的中点.files/image295.gif) ,连结
,连结.files/image297.gif) 、
、.files/image299.gif) .
.
.files/image301.gif) ∵
∵.files/image303.gif) ,
,
∴.files/image305.gif) .
.
∵.files/image307.gif) ,
,
∴.files/image309.gif) 平面
平面.files/image124.gif) .
.
∵.files/image312.gif) 平面
平面.files/image124.gif) ,
,
∴.files/image315.gif) .
…… 8分
.
…… 8分
∵.files/image317.gif)
∴.files/image319.gif) 平面
平面.files/image321.gif) .
.
∵.files/image323.gif) 平面
平面.files/image321.gif) ,
,
∴.files/image325.gif) .
.
∴∠.files/image327.gif) 是二面角
是二面角.files/image157.gif) 的平面角. ……10分
的平面角. ……10分
在Rt△.files/image133.gif) 中,
中, .files/image331.gif) ,
,
在Rt△.files/image321.gif) 中,
中, .files/image334.gif) ,
,
.files/image336.gif) . ……12分
. ……12分
∴ 二面角.files/image157.gif) 的平面角的余弦值是
的平面角的余弦值是.files/image338.gif) . ……14分
. ……14分
.files/image340.gif) 法2:建立如图所示的空间直角坐标系
法2:建立如图所示的空间直角坐标系.files/image342.gif) .
.
则.files/image344.gif) (-1,0,0),
(-1,0,0),.files/image056.gif) (-2,1,0),
(-2,1,0),.files/image104.gif) (0,0,1).
(0,0,1).
∴.files/image348.gif) =(-1,1,0),
=(-1,1,0),.files/image350.gif) =(1,0,1),
……8分
=(1,0,1),
……8分
设平面.files/image352.gif) 的法向量为
的法向量为.files/image354.gif) =(x,y,z),则:
=(x,y,z),则:
.files/image356.gif) ,
……10分
,
……10分
令.files/image358.gif) ,得
,得.files/image360.gif) ,
,
∴.files/image354.gif) =(1,1,-1).
=(1,1,-1).
显然,.files/image362.gif) 是平面
是平面.files/image364.gif) 的一个法向量,
的一个法向量,.files/image362.gif) =(
=(.files/image367.gif)
.files/image369.gif) ).
……12分
).
……12分
∴cos<.files/image354.gif) ,
,.files/image362.gif) >=
>=.files/image372.gif) .
.
∴二面角.files/image157.gif) 的平面角的余弦值是
的平面角的余弦值是.files/image338.gif) . ……14分
. ……14分
19. (本小题满分14分)
解:(1)依题意知,.files/image374.gif) …… 2分
…… 2分
∵.files/image376.gif) ,
,
∴.files/image378.gif) .
…… 4分
.
…… 4分
∴所求椭圆.files/image056.gif) 的方程为
的方程为.files/image380.gif) .
…… 6分
.
…… 6分
(2)∵ 点.files/image104.gif)
.files/image172.gif) 关于直线
关于直线.files/image174.gif) 的对称点为
的对称点为.files/image176.gif) ,
,
∴ .files/image383.gif) ……8分
……8分
解得:.files/image385.gif) ,
,.files/image387.gif) .
……10分
.
……10分
∴.files/image389.gif) .
……12分
.
……12分
∵
点.files/image104.gif)
.files/image172.gif) 在椭圆
在椭圆.files/image056.gif) :
:.files/image380.gif) 上,
上,
∴.files/image391.gif) , 则
, 则.files/image393.gif) .
.
∴.files/image178.gif) 的取值范围为
的取值范围为.files/image396.gif) .
……14分
.
……14分
20.(本小题满分14分)
解:(1)数表中前.files/image398.gif) 行共有
行共有.files/image400.gif) 个数,
个数,
即第i行的第一个数是.files/image184.gif) ,
…… 2分
,
…… 2分
∴.files/image180.gif) =
=.files/image403.gif) .
.
∵.files/image405.gif) ,
,.files/image180.gif) =2010,
=2010,
∴ i=11. …… 4分
令.files/image407.gif) ,
,
解得.files/image409.gif) .
…… 6分
.
…… 6分
(2)∵.files/image186.gif)
.files/image411.gif)
.files/image413.gif) .
…… 7分
.
…… 7分
∴.files/image415.gif) .
.
当.files/image417.gif) 时,
时, .files/image419.gif) , 则
, 则.files/image421.gif) ;
;
当.files/image423.gif) 时,
时, .files/image419.gif) , 则
, 则.files/image421.gif) ;
;
当.files/image427.gif) 时,
时, .files/image419.gif) , 则
, 则.files/image421.gif) ;
;
当.files/image430.gif) 时, 猜想:
时, 猜想:
.files/image432.gif) .
…… 11分
.
…… 11分
下面用数学归纳法证明猜想正确.
① 当.files/image434.gif) 时,
时,.files/image436.gif) , 即
, 即.files/image432.gif) 成立;
成立;
② 假设当.files/image439.gif) 时, 猜想成立,
即
时, 猜想成立,
即.files/image441.gif) ,
,
则.files/image443.gif) ,
,
∵.files/image445.gif) ,
,
∴.files/image447.gif) .
.
即当.files/image449.gif) 时,猜想也正确.
时,猜想也正确.
由①、②得当.files/image451.gif) 时,
时, .files/image432.gif) 成立.
成立.
当.files/image451.gif) 时,
时,.files/image455.gif)
.files/image194.gif) .
…… 13分
.
…… 13分
综上所述, 当.files/image458.gif) 时,
时, .files/image421.gif) ; 当
; 当.files/image451.gif) 时,
时,.files/image455.gif)
.files/image194.gif) .
…… 14分
.
…… 14分
另法( 证明当.files/image430.gif) 时,
时, .files/image432.gif) 可用下面的方法):
可用下面的方法):
当.files/image430.gif) 时,
时, .files/image460.gif) C
C.files/image462.gif) + C
+ C.files/image464.gif) + C
+ C.files/image466.gif) + C
+ C.files/image468.gif)
.files/image470.gif)
.files/image472.gif)
.files/image474.gif) .
.
21. (本小题满分14分)
解:(1)当.files/image201.gif) 时,
时,.files/image477.gif) ,
,
∴.files/image479.gif)
.files/image481.gif) .
.
令.files/image479.gif) =0, 得
=0, 得 .files/image483.gif) .
…… 2分
.
…… 2分
当.files/image485.gif) 时,
时,.files/image487.gif) , 则
, 则.files/image203.gif) 在
在.files/image490.gif) 上单调递增;
上单调递增;
当.files/image492.gif) 时,
时,.files/image494.gif) , 则
, 则.files/image203.gif) 在
在.files/image496.gif) 上单调递减;
上单调递减;
当.files/image498.gif) 时,
时,.files/image487.gif) ,
, .files/image203.gif) 在
在.files/image500.gif) 上单调递增.
…… 4分
上单调递增.
…… 4分
∴ 当.files/image502.gif) 时,
时, .files/image203.gif) 取得极大值为
取得极大值为.files/image505.gif)
.files/image507.gif) ;
;
当.files/image509.gif) 时,
时, .files/image203.gif) 取得极小值为
取得极小值为.files/image512.gif)
.files/image514.gif) . …… 6分
. …… 6分
(2) ∵ .files/image479.gif) =
= .files/image516.gif) ,
,
∴△= .files/image518.gif) =
= .files/image520.gif) .
.
① 若a≥1,则△≤0, …… 7分
∴.files/image479.gif) ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0).files/image522.gif) ,
,.files/image524.gif) ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. …… 9分
② 若a<1,则△>0,
∴.files/image479.gif) = 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
= 0有两个不相等的实数根,不妨设为x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
当.files/image018.gif) 变化时,
变化时,.files/image527.gif) 的取值情况如下表:
的取值情况如下表:
x
.files/image529.gif)
x1
(x1,x2)
x2
.files/image531.gif)
.files/image479.gif)
+
0
-
0
+
f(x)
ㄊ
极大值
ㄋ
极小值
ㄊ
…… 11分
∵.files/image533.gif) ,
,
∴.files/image535.gif) .
.
∴.files/image537.gif)
.files/image539.gif)
.files/image541.gif)
.files/image543.gif)
.files/image545.gif) .
.
同理.files/image547.gif)
.files/image549.gif) .
.
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com