
题目列表(包括答案和解析)
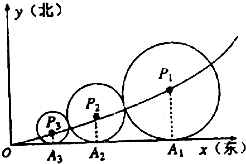 为建设好长、株、潭“两型社会”改革实验区,加快二市经济一体化进程,某规划部门在三市的交界处拟建一个大型环保生态公园,并在公园入口处的东南方位建造一个供市民休闲健身的小型绿化广场,如图是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道,设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,P(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,且这些圆型小道与主干道Ox分别于相切于A1,A2,…,An,…,且任意相邻的两圆彼此外切,若x1=1(单位:百米),且xn+1<xn.
为建设好长、株、潭“两型社会”改革实验区,加快二市经济一体化进程,某规划部门在三市的交界处拟建一个大型环保生态公园,并在公园入口处的东南方位建造一个供市民休闲健身的小型绿化广场,如图是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道,设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,P(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,且这些圆型小道与主干道Ox分别于相切于A1,A2,…,An,…,且任意相邻的两圆彼此外切,若x1=1(单位:百米),且xn+1<xn.| πS |
|
|
 .只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
.只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com