
题目列表(包括答案和解析)
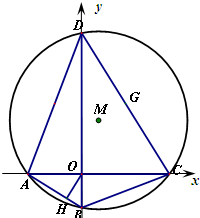 如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
如图,在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.| AB |
| AD |

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
 (2009•闸北区二模)和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.一般来说,在空间直角坐标系O-xyz中,空间曲面的方程是一个三元方程F(x,y,z)=0.
(2009•闸北区二模)和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹.一般来说,在空间直角坐标系O-xyz中,空间曲面的方程是一个三元方程F(x,y,z)=0.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com