
题目列表(包括答案和解析)
函数零点的概念
一般地,我们把使函数y=f(x)的________实数x称为函数y=f(x)的零点.
(2)描述法:把集合中的元素 的描述出来,写在 内表示集合的方法.一般形式是{x|p},其中竖线前面的x叫做此集合的代表元素,竖线后面的p指出元素x所具有的公共属性.描述法便于从整体上把握一个集合,常适用于集合中元素的公共属性较为明显时.
(3)韦恩图:为了形象地表示集合,有时常用一些封闭的 表示一个集合,这样的图形称为韦恩图,在解题时,利用韦恩图“数”和“形”结合,使得解答十分直观.?
如集合A={a,b,c}可形象地表示为图(1)或图(2).?
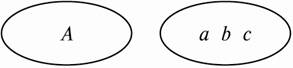
(1) (2)
互斥事件与事件的并
(1)互斥事件
________的两个事件叫做互斥事件(或称互不相容事件).
①不可能同时发生的两个事件A,B是指如果A发生,则B________;如果B发生,则A________.
②类比集合,可用图表示如:
③推广:如果事件A1,A2,…,An之间任意两个都互斥,就称事件A1,A2,…,An________.
(2)事件的并
一般地,事件A和B________(即A发生,或B发生,或A,B都发生),则由事件A与B所构成的事件C,称为事件A与B的并(或和).
①事件A与B的并记作________.
②类比集合:________.
③事件A与事件B的________事件B与事件A的并,即________.
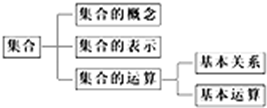
| A、“集合的概念”的下位 | B、“集合的表示”的下位 | C、“基本关系”的下位 | D、“基本运算”的下位 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com