
题目列表(包括答案和解析)
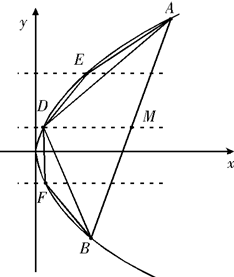 (2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
(2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.| 16(1-kb) | k2 |
| 1-1 | 1-2 | 4-1 | |
| 男生 | 75 | a | 40 |
| 女生 | b | 50 | 30 |
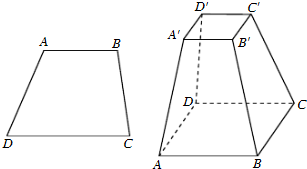 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.| x |
| x+h |
| a |
| b |
| ah |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
| 1 |
| 3 |
| 4-4 | 4-5 | 4-7 | |
| 男生 | 130 | a | 80 |
| 女生 | b | 100 | 60 |
| 1-1 | 1-2 | 4-1 | |
| 男生 | 75 | a | 40 |
| 女生 | b | 50 | 30 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com