
题目列表(包括答案和解析)
(08年成都七中二模文) 设函数f(x)=![]() 的图像关于原点对称,f(x)的图像在点P(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.
的图像关于原点对称,f(x)的图像在点P(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.
(1)求a、b、c、d的值;
(2)若x1、x2∈[-1,1],求证:|f(x1) -f(x2)≤![]() .
.
(1)f(x)=x + ![]() 的值域为[3,9],K
的值域为[3,9],K![]() [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
(2)g (x) =x+2+![]() 的值域为[7,11],K
的值域为[7,11],K![]() [7,11]时,g(x)=K
[7,11]时,g(x)=K
也有两不等根x3、x4,求x3+x4
(3)h(x) =x+![]() -b , x>a
-b , x>a
h(x)=K的两根之和为K+18,且h(x)的最小值为0,试求a与b的值。
(本小题满分12分)已知![]() =(cos+sin,-sin),
=(cos+sin,-sin),![]() =(cos-sin,2cos).
=(cos-sin,2cos).
(1)设f(x)=![]() ·
·![]() ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈,且f(x1)=f(x2)=1,求x1+x2的值.
(12分)(1)设x、y、z R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥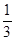 ;
;
(2)设二次函数f (x)=ax2+bx+c (a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2< ,若x
,若x (0,x1)。
(0,x1)。
求证:x<f (x)<x1
(本小题满分12分)
已知 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈ ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com