
题目列表(包括答案和解析)
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数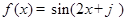 和
和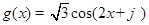 .
.
(Ⅰ)设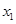 是
是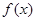 的极大值点,
的极大值点,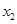 是
是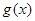 的极小值点,求
的极小值点,求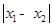 的最小值;
的最小值;
(Ⅱ)若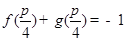 ,且
,且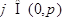 ,求
,求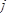 的值.
的值.
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数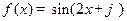 和
和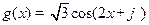 .
.
(Ⅰ)设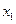 是
是 的极大值点,
的极大值点, 是
是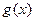 的极小值点,求
的极小值点,求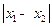 的最小值;
的最小值;
(Ⅱ)若 ,且
,且 ,求
,求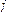 的值.
的值.
四.本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令X表示此人选对A饮料的杯数.假设次人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
(本小题满13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)已知函数![]() 的定义域是
的定义域是![]() ,函数
,函数![]() 的定义域是
的定义域是![]() .
.
(Ⅰ) 求集合![]() ; (Ⅱ)若
; (Ⅱ)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16. (本小题满分12分)
已知向量 ,定义函数
,定义函数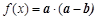
(Ⅰ)求函数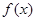 最小正周期;
最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com