
题目列表(包括答案和解析)
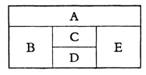
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.
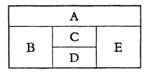
①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为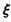 求
求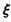 的分布列和数学期望E
的分布列和数学期望E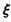
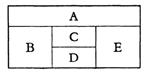
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.
①求恰有两个区域用红色鲜花的概率;
 ②记花圃中红色鲜花区域的块数为
②记花圃中红色鲜花区域的块数为![]() 求
求![]() 的分布列和数学期望E
的分布列和数学期望E![]()
 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率; 求
求 的分布列和数
的分布列和数 学期望E
学期望E
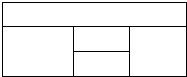 [理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
[理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花. [理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
[理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com