
题目列表(包括答案和解析)
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
|
男 |
女 |
总计 |
|
爱好 |
40 |
20 |
60 |
|
不爱好 |
20 |
30 |
50 |
|
总计 |
60 |
50 |
110 |
由K2= 算得,K2=
算得,K2=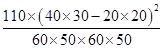 ≈7.8.
≈7.8.
附表:
|
P(K2≥k) |
0.050 |
0.010 |
0.001 |
|
k |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
| 男 | 女 | 合计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 3 | 50 |
| 合计 | 60 | 50 | 110 |
由χ2=![]() 算得
算得
χ2=![]() ≈7.8
≈7.8
得到的正确结论是( )
(A)认为“爱好该项运动与性别有关”为错误结论的可能性为5%
(B)认为“爱好该项运动与性别无关”为错误结论的可能性为5%
(C)有99%的把握认为“爱好该项运动和性别有关”
(D)有99%的把握认为“爱好该项运动和性别无关”
设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使|A1B1|=|A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A.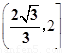 B.
B.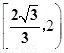
C.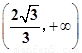 D.
D. 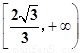
如图,在直三棱柱 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形, ,
, 为棱
为棱 上一点,且平面
上一点,且平面 平面
平面 .
.
(Ⅰ)求证: 点为棱
点为棱 的中点;
的中点;
(Ⅱ)判断四棱锥 和
和 的体积是否相等,并证明。
的体积是否相等,并证明。

【解析】本试题主要考查了立体几何中的体积问题的运用。第一问中,
易知 ,
, 面
面 。由此知:
。由此知: 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
的中点.
(2)中由A1B1⊥平面B1C1CD,BC⊥平面A1ABD,D为BB1中点,可以得证。
(1)过点 作
作 于
于 点,取
点,取 的中点
的中点 ,连
,连 。
。 面
面 面
面 且相交于
且相交于 ,面
,面 内的直线
内的直线 ,
, 面
面 。……3分
。……3分
又 面
面 面
面 且相交于
且相交于 ,且
,且 为等腰三角形,易知
为等腰三角形,易知 ,
, 面
面 。由此知:
。由此知: ,从而有
,从而有 共面,又易知
共面,又易知 面
面 ,故有
,故有 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
…6分
的中点.
…6分
(2)相等.ABC-A1B1C1为直三棱柱,∴BB1⊥A1B1,BB1⊥BC,又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)∴VA1-B1C1CD=1 /3 SB1C1CD•A1B1=1/ 3 ×1 2 (B1D+CC1)×B1C1×A1B1VC-A1ABD=1 /3 SA1ABD•BC=1 /3 ×1 2 (BD+AA1)×AB×BC∵D为BB1中点,∴VA1-B1C1CD=VC-A1ABD
观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)= ( )
| A.f(x) | B.-f(x) | C.g(x) | D.-g(x) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com