注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
方案一:甲队单独完成这项工程刚好能够如期完成;
方案二:乙队单独完成这项工程要比规定的时间多用10天;
方案三:若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成.
又从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元.
试问,在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
解题方案:
设甲队单独完成需x天,则乙队单独完成需(x+10)天.
(1)用含x的代数式表示:
甲队每天可以完成这项工程的工作量是工程总量的
乙队每天可以完成这项工程的工作量是工程总量的
根据题意,列出相应方程
解这个方程,得
x=40
x=40
检验:
x=40是原方程的根
x=40是原方程的根
(2)方案一得工程款为
40×1.5=60(万元)
40×1.5=60(万元)
;
方案二不合题意,舍去
方案三的工程款为
8×1.5+40×1.1=56(万元)
8×1.5+40×1.1=56(万元)
所以在不耽误工期的前提下,应选择方
(3)
(3)
能节省工程款.

 (2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
(2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.

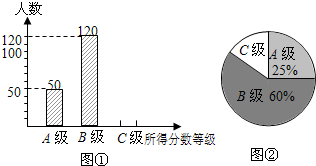 <8;C级:0≤x<4,并将调查结果绘制成图①和图②的统计图(不完整).
<8;C级:0≤x<4,并将调查结果绘制成图①和图②的统计图(不完整).