
题目列表(包括答案和解析)
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
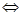
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
已知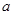 ,
,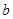 ,
,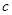 分别为
分别为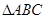 三个内角
三个内角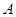 ,
,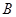 ,
,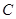 的对边,
的对边, .
.
(Ⅰ)求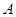 ;
;
(Ⅱ)若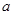 =2,
=2,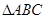 的面积为
的面积为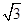 ,求
,求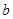 ,
,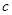 .
.
【命题意图】本题主要考查正余弦定理应用,是简单题.
【解析】(Ⅰ)由 及正弦定理得
及正弦定理得
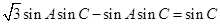
由于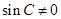 ,所以
,所以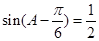 ,
,
又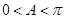 ,故
,故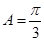 .
.
(Ⅱ) 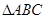 的面积
的面积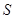 =
=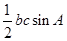 =
=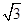 ,故
,故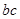 =4,
=4,
而 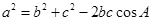 故
故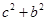 =8,解得
=8,解得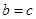 =2
=2
设抛物线 :
: (
( >0)的焦点为
>0)的焦点为 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以 为圆心,
为圆心, 为半径的圆
为半径的圆 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为 ,求
,求 的值及圆
的值及圆 的方程;
的方程;
(Ⅱ)若 ,
, ,
, 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
= ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|= ,
,
∵ 的面积为
的面积为 ,∴
,∴ =
= =
= =
= ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
, 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点 对称得:
对称得:
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
在下列各命题中:
①|a+b|-|a-b|≤2|b|;
②a、b∈R+,且x≠0,则|ax+![]() |≥2
|≥2![]() ;
;
③若|x-y|<ε,则|x|<|y|+ε;
④当且仅当ab<0或ab=0时,|a|-|b|≤|a+b|中的等号成立.
其中真命题的序号为__________.
本题主要考查绝对值不等式|a|-|b|≤|a±b|≤|a|+|b|的应用.
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com