
题目列表(包括答案和解析)
已知函数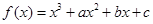 在
在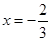 与
与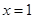 时都取得极值.
时都取得极值.
(1)求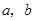 的值及函数
的值及函数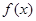 的单调区间;www.7caiedu.cn
的单调区间;www.7caiedu.cn
(2)若对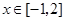 ,不等式
,不等式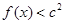 恒成立,求
恒成立,求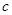 的取值范围.
的取值范围.
【解析】根据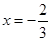 与
与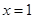 是
是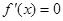 的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
(2)此题本质是利用导数其函数f(x)在区间[-1,2]上的最大值,然后利用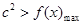 ,即可解出c的取值范围.
,即可解出c的取值范围.
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.

【解析】(1)证:DE//BF即可;
(2)可以利用向量法根据二面角P-BF-C的余弦值为 ,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |

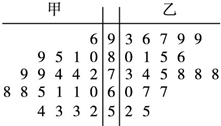 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11 n22-n12n21)2 |
| n1+ n2+n+1n+2 |
| P(k2≥K) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com