
题目列表(包括答案和解析)
如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 的一点,
的一点, ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线 与
与 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一问中,利用建立空间直角坐标系
解:(I)以B为原点, 、
、 分别为Y,Z轴建立空间直角坐标系.由于,
分别为Y,Z轴建立空间直角坐标系.由于,

在三棱柱 中有
中有
 ,
,
设


又 侧面
侧面 ,故
,故 . 因此
. 因此 是异面直线
是异面直线 的公垂线,则
的公垂线,则 ,故异面直线
,故异面直线 的距离为1.
的距离为1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小为向量
的大小为向量 与
与 的夹角.
的夹角.

已知![]() 有极大值又有极小值,则
有极大值又有极小值,则![]() 的取值范围是 。
的取值范围是 。
已知 有极大值又有极小值,则
有极大值又有极小值,则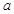 取值范围是____
取值范围是____
已知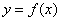 有反函数
有反函数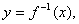 又
又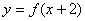 与
与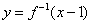 互为反函数,则
互为反函数,则
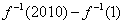 的值为_____ ____.
的值为_____ ____.
已知曲线 的参数方程是
的参数方程是 (
( 是参数),以坐标原点为极点,
是参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 :的极坐标方程是
:的极坐标方程是 =2,正方形ABCD的顶点都在
=2,正方形ABCD的顶点都在 上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2, ).
).
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
【命题意图】本题考查了参数方程与极坐标,是容易题型.
【解析】(Ⅰ)由已知可得 ,
, ,
,
 ,
, ,
,
即A(1, ),B(-
),B(- ,1),C(―1,―
,1),C(―1,― ),D(
),D( ,-1),
,-1),
(Ⅱ)设 ,令
,令 =
= ,
,
则 =
= =
= ,
,
∵ ,∴
,∴ 的取值范围是[32,52]
的取值范围是[32,52]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com