
题目列表(包括答案和解析)
[2012·江西卷] 如图1-7,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4![]() ,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
,DE=4,现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合于点G,得到多面体CDEFG.
(1)求证:平面DEG⊥平面CFG;
(2)求多面体CDEFG的体积.
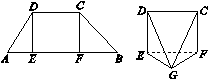
图1-7
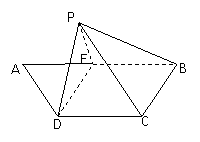
(08年东北师大附中) 已知梯形ABCD,AB//CD,AD=CD=BC=![]() AB=1,E为AB的中点,将△ADE沿DE折起使点A至点P,且平面PDE⊥平面DEBC,则点D到平面PBC的距离是
AB=1,E为AB的中点,将△ADE沿DE折起使点A至点P,且平面PDE⊥平面DEBC,则点D到平面PBC的距离是
(A) | (B) | (C) | (D) |
在空间四边形ABCD中,已知AD=1,BC=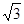 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD=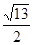 ,AC=
,AC=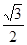 , AC和BD所成的角是( )
, AC和BD所成的角是( )
A.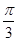 B.
B.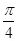 C.
C.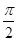 D.
D.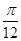
空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.
求证:四边形EFGH为平行四边形;
E在AB的何处时截面EFGH的面积最大?最大面积是多少?
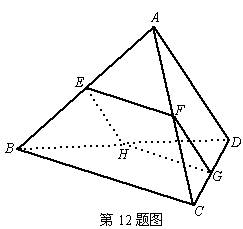
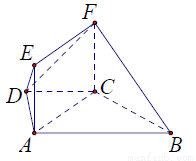
如图所示,多面体EF﹣ABCD中,底面ABCD为等腰梯形,AB∥CD,四边形ACFE为矩形,且平面ACFE⊥平面ABCD,AD=DC=BC=CF=1,AC⊥BC,∠ADC=120°
(1)求证:BC⊥AF
(2)求平面BDF与平面CDF所成夹角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com