课外研究题：将一块圆心角为，半径为20厘米的扇形铁片裁成一块矩形，请你设计裁法，使裁得矩形的面积最大?并说明理由．

教学建议：这是一个研究性学习内容，可让学生在课外两人一组合作完成，写成研究报告，在习题课上让学生交流研究结果，老师可适当进行点评。

参考答案：这是一个如何下料的问题，一般有如图（1）、图（2）的两种裁法：即让矩形一边在扇形的一条半径上，或让矩形一边与弦平行。从图形的特点来看，涉及到线段的长度和角度，将这些量放置在三角形中，通过解三角形求出矩形的边长，再计算出两种方案所得矩形的最大面积，加以比较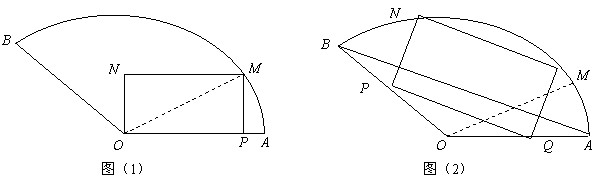，就可以得出问题的结论．

一口袋内装有5个黄球，3个红球，现从袋中往外取球，每次取出一个，取出后记下球的颜色，然后放回，直到红球出现10次时停止，停止时取球的次数是一个随机变量，则=______________。（填计算式）

 [解题思路]：这是一个“12次独立重复试验恰有10次发生”的概率问题，同学们很容易由二项分布原理得到，这就忽视了隐含条件“第12次抽取的是红球”，此种解法的结果包含着第12次抽取到黄球。

如果执行右边的程序框图，输入正整数N(N≥2)和实数a₁,a₂,…,a_N，输出A,B，则

（A）A+B为a₁,a₂,…,a_N的和

（B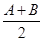）为a₁,a₂,…,a_N的算术平均数

（C）A和B分别是a₁,a₂,…,a_N中最大的数和最小的数

（D）A和B分别是a₁,a₂,…,a_N中最小的数和最大的数

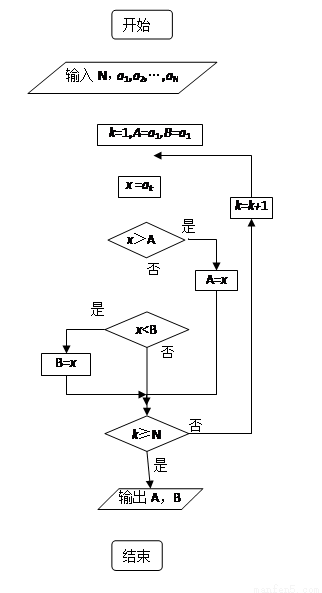
【解析】根据程序框图可知，这是一个数据大小比较的程序，其中A为最大值，B为最小值，选C.

 

A、“若a，b，c是等比数列，则b2=ac”的逆命题

B、“平行于同一条直线的两条直线平行，若a∥c，b∥c，则a∥b”这是一个“三段论”

C、“?x∈R，x2+1≥1”的否定

D、“向量 a = 0 ， b = 0 ”是“ a • b =0”的充要条件

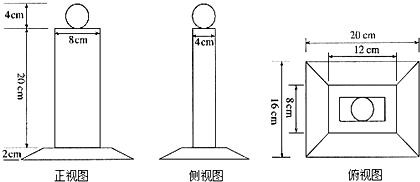如图，这是一个奖杯的三视图，（1）请你说明这个奖杯是由哪些基本几何体组成的；
（2）求出这个奖杯的体积．