
题目列表(包括答案和解析)
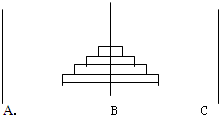 如图,汉诺塔问题是指有3根杆子A.B.C,B杆上有若干碟子,把所有碟子从B杆移到C杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到C杆上,最少需要移动( )次.
如图,汉诺塔问题是指有3根杆子A.B.C,B杆上有若干碟子,把所有碟子从B杆移到C杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到C杆上,最少需要移动( )次.如图,汉诺塔问题是指有3根杆子A,B,C,杆上有若干碟子,把所有的碟子从B杆移![]() 到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )
到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的3个碟子全部移动到A杆上,则最少需要移动的次数是( )

A.12 B.9 C.6 D.7
如图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面,把B杆上的4个碟子全部移到A杆上,最少需要移动次
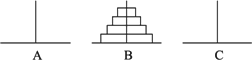
12
15
17
19
如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动________次.
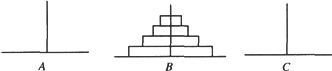
A.12
B.15
C.17
D.19
如下图所示,汉诺塔问题是指有3根杆子A、B、C、D杆上有若干碟子,把所有碟子借助于C杆从B杆移到A杆上,每次只能移动1个碟子,大的碟子不能叠在小的碟子上面.现把B杆上的4个碟子全部移到A杆上,至少需要移动多少次

A.12
B.15
C.17
D.19
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com