
题目列表(包括答案和解析)
| nπ |
| 3 |
| 1 |
| 2 |
“鸡兔同笼“是我国隋朝时期的数学著作《孙子算经》中的一个有趣而具有深远影响的题目:
“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何。
用方程组的思想不难解决这一问题,请你设计一个这类问题的通用算法。
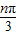 ,n=1,2,3,…
,n=1,2,3,… ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何.”
用方程组的思想不难解决这一问题,请你设计一个这类问题的通用算法.
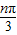 ,n=1,2,3,…
,n=1,2,3,… ),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.
),且an+1=2an(1-an),n∈N*,判断数列{an}是否为周期数列,并证明你的结论.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com