如图所示，顶角=45°，的金属导轨MON固定在水平面内，导轨处在方向竖直、磁感应强度为 B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度0 v 沿导轨 MON向左滑动，导体棒的质量为m，导轨与导体棒单位长度的电阻均匀为r.导体棒与导轨接触点的a和b，导体棒在滑动过程中始终保持与导轨良好接触.t=0时，导体棒位于顶角O处，求：

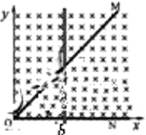（1）t时刻流过导体棒的电流强度I和电流方向。

（2）导体棒作匀速直线运动时水平外力F的表达式。

（3）导体棒在O～t时间内产生的焦耳热Q。
（4）若在to时刻将外力 F撤去，导体棒最终在导轨上静止时的坐标 x。

如图所示，顶角θ=45°，的金属导轨 MON固定在水平面内，导轨处在方向竖直．磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v₀沿导轨MON向左滑动，导体棒的质量为m，导轨与导体棒单位长度的电阻均匀为r.导体棒在滑动过程中始终保持与导轨良好接触.t=0时，导体棒位于顶角O处，求：

   （1）t时刻流过导体棒的电流强度I和电流方向.

   （2）导体棒作匀速直线运动时水平外力F的表达式.

   （3）闭合回路在0～t时间内产生的焦耳热Q.

   （4）若在t₀时刻将外力F撤去，导体棒最终在导轨上静止时的坐标x.

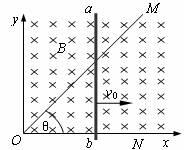
图16-7

(1)t时刻流过导体棒的电流强度I和电流方向;

(2)导体棒做匀速直线运动时水平外力F的表达式；

(3)导体棒在0—t时间内产生的焦耳热Q；

(4)若在t₀时刻将外力F撤去，导体棒最终在导轨上静止时的坐标x.

如图所示，一端封闭的两条平行光滑长导轨相距L，距左端L处的右侧一段弯成半径为的四分之一圆弧，圆弧导轨的左、右两段处于高度相差的水平面上。以弧形导轨的末端点O为坐标原点，水平向右为x轴正方向，建立Ox坐标轴。圆弧导轨所在区域无磁场；左段区域存在空间上均匀分布，但随时间t均匀变化的磁场B（t），如图2所示；右段区域存在磁感应强度大小不随时间变化，只沿x方向均匀变化的磁场B（x），如图3所示；磁场B（t）和B（x）的方向均竖直向上。在圆弧导轨最上端，放置一质量为m的金属棒ab，与导轨左段形成闭合回路，金属棒由静止开始下滑时左段磁场B（t）开始变化，金属棒与导轨始终接触良好，经过时间t₀金属棒恰好滑到圆弧导轨底端。已知金属棒在回路中的电阻为R，导轨电阻不计，重力加速度为g。

（1）求金属棒在圆弧轨道上滑动过程中，回路中产生的感应电动势E；

（2）如果根据已知条件，金属棒能离开右段磁场B（x）区域，离开时的速度为v，求金属棒从开始滑动到离开右段磁场过程中产生的焦耳热Q;

（3）如果根据已知条件，金属棒滑行到x=x₁，位置时停下来，

a．求金属棒在水平轨道上滑动过程中遁过导体棒的电荷量q；

b．通过计算，确定金属棒在全部运动过程中感应电流最大时的位置。

如图所示，一端封闭的两条平行光滑长导轨相距L，距左端L处的右侧一段弯成半径为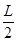的四分之一圆弧，圆弧导轨的左、右两段处于高度相差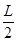的水平面上。以弧形导轨的末端点O为坐标原点，水平向右为x轴正方向，建立Ox坐标轴。圆弧导轨所在区域无磁场；左段区域存在空间上均匀分布，但随时间t均匀变化的磁场B（t），如图2所示；右段区域存在磁感应强度大小不随时间变化，只沿x方向均匀变化的磁场B（x），如图3所示；磁场B（t）和B（x）的方向均竖直向上。在圆弧导轨最上端，放置一质量为m的金属棒ab，与导轨左段形成闭合回路，金属棒由静止开始下滑时左段磁场B（t）开始变化，金属棒与导轨始终接触良好，经过时间t₀金属棒恰好滑到圆弧导轨底端。已知金属棒在回路中的电阻为R，导轨电阻不计，重力加速度为g。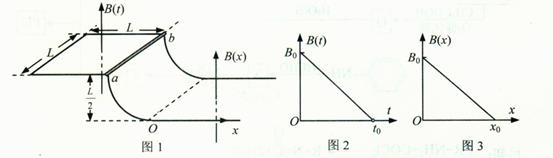

（1）求金属棒在圆弧轨道上滑动过程中，回路中产生的感应电动势E；
（2）如果根据已知条件，金属棒能离开右段磁场B（x）区域，离开时的速度为v，求金属棒从开始滑动到离开右段磁场过程中产生的焦耳热Q;
（3）如果根据已知条件，金属棒滑行到x=x₁，位置时停下来，
a．求金属棒在水平轨道上滑动过程中遁过导体棒的电荷量q；
b．通过计算，确定金属棒在全部运动过程中感应电流最大时的位置。