
题目列表(包括答案和解析)
、出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中,点还是形如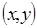 的有序实数对,直线还是满足
的有序实数对,直线还是满足 的所有
的所有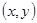 组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点 定义它们之间的一种“距离”:
定义它们之间的一种“距离”: ,请解决以下问题:
,请解决以下问题:
1、(理)求线段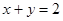
 上一点
上一点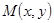 的距离到原点
的距离到原点 的“距离”;
的“距离”;
(文)求点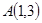 、
、 的“距离”
的“距离” ;
;
2、(理)定义:“圆”是所有到定点“距离”为定值的点组成的图形,
求“圆周”上的所有点到点 的“距离”均为
的“距离”均为 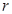 的“圆”方程;
的“圆”方程;
(文)求线段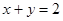
 上一点
上一点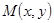 的距离到原点
的距离到原点 的“距离”;
的“距离”;
3、(理)点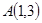 、
、 ,写出线段
,写出线段 的垂直平分线的轨迹方程并画出大致图像.
的垂直平分线的轨迹方程并画出大致图像.
(文)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点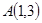 、
、 ,
, ,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
(说明所给图形小正方形的单位是1)

 的有序实数对,直线还是满足
的有序实数对,直线还是满足 的所有
的所有 组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点 定义它们之间的一种“距离”:
定义它们之间的一种“距离”: ,请解决以下问题:
,请解决以下问题:
 上一点
上一点 的距离到原点
的距离到原点 的“距离”;
的“距离”; 、
、 的“距离”
的“距离” ;
; 的“距离”均为
的“距离”均为  的“圆”方程;
的“圆”方程;
 上一点
上一点 的距离到原点
的距离到原点 的“距离”;
的“距离”; 、
、 ,写出线段
,写出线段 的垂直平分线的轨迹方程并画出大致图像.
的垂直平分线的轨迹方程并画出大致图像. 、
、 ,
, ,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
,求经过这三个点确定的一个“圆”的方程,并画出大致图像; 
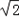 ,0)和(0,2),求椭圆C1的标准方程;
,0)和(0,2),求椭圆C1的标准方程;| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com