当今的时代是计算机时代，我们知道计算机装置有一数据输入口A和一个运算结果的输出口

B．某同学编入下列运算程序将数据输入且满足以下性质：(1)从A输入1时，从B得到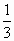；(2)从A输入整数n(n≥2)时，在B得到的结果f(n)是将前一结果f(n－1)先乘以奇数2n－3，再除以奇数2n＋1．试问：

(Ⅰ)从A输入2，3，4时，从B分别得到什么数？

(Ⅱ)从A输入1，2，3，……2002时，从B得到的各数之和是多少？并说明理由．

设椭圆的左、右顶点分别为，点在椭圆上且异于两点，为坐标原点.

（Ⅰ）若直线与的斜率之积为，求椭圆的离心率；

（Ⅱ）若，证明直线的斜率 满足

【解析】(1)解：设点P的坐标为.由题意，有  ①

由，得，

由，可得，代入①并整理得

由于，故.于是，所以椭圆的离心率

（2）证明：（方法一）

依题意，直线OP的方程为，设点P的坐标为.

由条件得消去并整理得  ②

由，及，

得.

整理得.而，于是，代入②，

整理得

由，故，因此.

所以.

(方法二)

依题意，直线OP的方程为，设点P的坐标为.

由P在椭圆上，有

因为，，所以，即   ③

由，，得整理得.

于是，代入③，

整理得

解得，

所以.