练习册

  • 练习册
  • 试题
    【查看更多】

     

    题目列表(包括答案和解析)

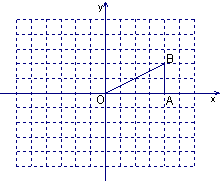
    （本小题满分12分）如图，在平面直角坐标系中，直线：与轴交于点，与轴交于点，抛物线过点、点，且与轴的另一交点为，其中＞0，又点是抛物线的对称轴上一动点．

    （1）求点的坐标，并在图1中的上找一点，使到点与点的距离之和最小；

    （2）若△周长的最小值为，求抛物线的解析式及顶点的坐标；

    （3）如图2，在线段上有一动点以每秒2个单位的速度从点向点移动(不与端点、重合)，过点作∥交轴于点,设移动的时间为秒，试把△的面积表示成时间的函数，当为何值时，有最大值，并求出最大值.

     

    查看答案和解析>>

    （本小题满分12分）

    如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN ∥OB交CD于N．

    1.⑴求证：MN是⊙O的切线；

    2.⑵当0B=6cm，OC=8cm时，求⊙O的半径及图中阴影部分的面积．

     

    查看答案和解析>>

    （本小题满分12分）

    甲、乙、丙三个人准备打羽毛球，他们约定用“抛硬币”的方式来确定哪两个人先上场，三人手中各持有一枚质地均匀的硬币，同时将手中硬币抛落到水平地面为一个回合．落地后，三枚硬币中，恰有两枚正面向上或反面向上的这两枚硬币持有人先上场；若三枚硬币均为正面向上或反面向上，属于不能确定．

    1.（1）请你画出表示“抛硬币”一个回合所有可能出现的结果的树状图；

    2.（2）求一个回合能确定两人先上场的概率．

     

    查看答案和解析>>

    （本小题满分12分）

    如图，在Rt△OAB中，∠OAB＝90°，且点B的坐标为（4，2）．

    1.⑴ 画出关于点O成中心对称的，并写出点B1的坐标；

    2.⑵ 求出以点B1为顶点，并经过点B的二次函数关系式．

     

    查看答案和解析>>

     （本小题满分12分）

    如图，RtΔABC中，∠ACB=90°，AC=4，BA=5，点P是AC上的动点（P不与A、C重合）PQ⊥AB，垂足为Q．设PC=x，PQ= y．

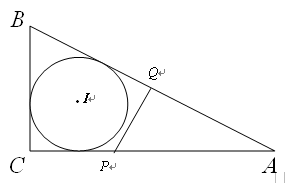
    1.⑴求y与x的函数关系式；

    2.⑵试确定此RtΔABC内切圆I的半径，并探求x为何值时，直线PQ与这个内切圆I相切？

    3.⑶若0<x<1，试判断以P为圆心，半径为y的圆与⊙I能否相内切，若能求出相应的x的值，若不能，请说明理由．

     

    查看答案和解析>>

    一　选择题(共20分，每小题2分)

    1. B  2 . B  3. C　4 .Ａ  5 Ｃ  6 . C   7. Ｃ   8. Ａ   9 . B   10.  D

    .

    二，填空题。（共24分，每小题3分）

    11 .  12 .    13 .     14 .   15.    16 .  17 .  18 ..

    三、

    19解：

     

     

     

     

    当时，原式=（）

    20（1）如图

     

     

     

     

     

     

     

     

    （2）优等人数为 

         良等人数为 

    （3）优、良等级的概率分别是   

    （4）该校数学成绩优等、良等人数共占40%、等人数仅占10%，说明该校期末考试成绩比较好．（只要合理，均给分）

    21.解: （1）∵在Rt△AOB中，∠AOB＝900，∠ABO＝600，OB＝1

            ∴AB＝2，OA＝

                  ∴点A坐标

     

    ∵二次函数y=ax2+bx+c的图像经过点A、点B和点C

    ∴

      解得

    ∴该二次函数的表达式

    （2）对称轴为；顶点坐标为．

    （3）∵对称轴为，A

    ∴点D坐标

    ∴四边形ABCD为等腰梯形

    22.解：过点D作DE⊥BC交BC延长线于点E，过点E作EF∥AD交AB于点F

    在Rt△CDE中，∠CED=90°,∠DCE=30°,CD=10

    ∴DE=5,  CE=

    ∴BE=

    ∵太阳光线AD与水平地面成30°角

    ∴∠FEB=30°

    在Rt△BFE中，∠B=90°,∠FEB=30°,BE=

    ∴BF=BE?tan∠FEB==

    ∵AF=DE=5

    ∴AB=AF+BF===19.1≈19

    答旗杆AB的高度为19米.

     

    23解：⑴

    ⑵如图所示

     

     

     

    ⑶如图所示

     

     

     

     

    24.解：(1)如图1，AE=AF. 理由：证明△ABE≌△ADF(ASA)

    (2)如图2, PE=PF.

    理由：过点P作PM⊥BC于M，PN⊥DC于N，则PM=PN.由此可证得△PME≌△PNF(ASA)，从而证得PE=PF.

          (3) PE、PF不具有（2）中的数量关系.

    当点P在AC的中点时，PE、PF才具有（2）中的数量关系.

    25.解：（1）由已知条件，得

      （2）由已知条件，得

          

          解得   

        

     

    ∴应从A村运到甲库50吨，运到乙库150吨；从B村运到甲库190吨，运到乙库110吨，这样调运就能使总运费最少.

    （3）这个同学说的对.

    理由：设A村的运费为元，则，

    ∴当x=200时，A村的运费最少，

    而y=-2x+9680(0≤x≤200)

    ∵K=-2＜0

    ∴X=200时，y有最小值，两村的总运费也是最少。

    即当x=200时，A村和两村的总运费都最少。

    26.解：（1）如图，作DE⊥AB于E，CF⊥AB于F,

    依题意可知，四边形CDEF是矩形，AE=BF,

    在Rt△ADE中，

    ∴梯形ABCD的周长为, 面积为.

    （2）∵PQ平分梯形ABCD的周长，

    ∴

    解得

    ∴当PQ平分梯形ABCD的周长时，

    （3）∵PQ平分梯形ABCD的面积

    ∴①当点P在AD边上时，

    解得

    ②当点P在DC边上时，

    即

    解得

    ③当点P在CB边上时，

    ∵△<0,∴此方程无解.

    ∴当PQ平分梯形ABCD的面积时，

    （4）.

     

     


    同步练习册答案