
题目列表(包括答案和解析)
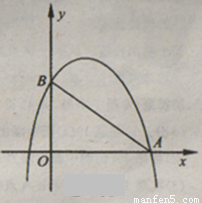
如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
1.求此二次函数关系式和点B的坐标;
2.在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【解析】
3.把点A的坐标代入二次函数,求出b的值,确定二次函数关系式,把x=0代入二次函数求出点B的坐标.
4.分情况讨论,①当BP=AP时,②当AB=AP时,分别求出即可得出答案.
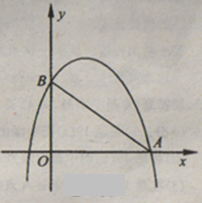
如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
1.求此二次函数关系式和点B的坐标;
2.在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【解析】
3.把点A的坐标代入二次函数,求出b的值,确定二次函数关系式,把x=0代入二次函数求出点B的坐标.
4.分情况讨论,①当BP=AP时,②当AB=AP时,分别求出即可得出答案.
| (2x-y)2 |
| 3 | (x-2y)3 |
| 3x+y |
| x-y |
| (2x-y)2 |
| 3 | (x-2y)3 |
|
|
| 3x+y |
| x-y |
| 3x+y |
| x-y |
问题情境:
用同样大小的黑色棋子按如图所示的规律摆放,则第2012个图共有多少枚棋子?

建立模型:
有些规律问题可以借助函数思想来探讨,具体步骤:第一步,确定变量;第二步:在直角坐标系中画出函数图象;第三步:根据函数图象猜想并求出函数关系式;第四步:把另外的某一点代入验证,若成立,则用这个关系式去求解.
解决问题:
根据以上步骤,请你解答“问题情境”.

【解析】此题把规律问题借助函数思想来探讨,主要培养学生的应变能力和空间想象能力
| (2x-y)2 |
| 3 | (x-2y)3 |
| 3x+y |
| x-y |
| (2x-y)2 |
| 3 | (x-2y)3 |
|
|
| 3x+y |
| x-y |
| 3x+y |
| x-y |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com