练习册

  • 练习册
  • 试题
    已知定点A.动点B是圆(F为圆心)上一点.动点P满足.. (Ⅰ)求动点P的轨迹方程, 【查看更多】

     

    题目列表(包括答案和解析)

    已知定点A（－2，0），动点B是圆（F为圆心）上一点，线段AB的垂直平分线交BF于P.

       （1）求动点P的轨迹方程；

       （2）是否存在过点E（0，－4）的直线l交P点的轨迹于点R，T，且满足 （O为原点），若存在，求直线l的方程，若不存在，请说明理由.

    查看答案和解析>>

    已知定点A（－2，0），动点B是圆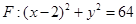（F为圆心）上一点，线段AB的垂直平分线交BF于P．w.w.w.zxxk.c.o.m         

    （I）求动点P的轨迹方程；

    （II）是否存在过点E（0，－4）的直线l交P点的轨迹于点R，T，  且满足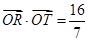（O为原点）．若存在，求直线l的方程；若不存在，请说明理由．

     

    查看答案和解析>>

    已知定点A（－2，0），动点B是圆F：（F为圆心）上一点，线段AB的垂直平分线交BF于P.

       （1）求动点P的轨迹E的方程；

       （2）直线交于M，N两点，试问在曲线E位于第二象限部分上是否存在一点C，使共线（O为坐标原点）？若存在，求出点C的坐标；若不存在，请说明理由.

    查看答案和解析>>

    已知定点A（－2，0），动点B是圆F：（F为圆心）上一点，线段AB的垂直平分线交BF于P.

       （1）求动点P的轨迹E的方程；

       （2）点C是曲线E位于第二象限部分上的点，且满足共线，求点C的坐标。

    查看答案和解析>>

    已知定点A（－2，0），动点B是圆F：（F为圆心）上一点，线段AB的垂直平分线交BF于P.

    （1）求动点P的轨迹E的方程；

    （2）直线交于M，N两点，试问在曲线E位于第二象限部分上

    是否存在一点C，使共线（O为坐标原点）？若存在，求出点C的坐标；若不存在，请说明理由.

    查看答案和解析>>

    一、选择题   D C C C A    C B CAB   D B

    二、填空题  13. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 14. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 15. -8  16. 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    三、解答题

    17.(10分)  解：（Ⅰ）由已知得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由余弦定理得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………3分

    因为锐角△ABC中，A＋B＋C＝p，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………6分

    （Ⅱ）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．将高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。代入余弦定理：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。解得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．…10分

    18.（12分） 解：（Ⅰ）依题意，当甲连胜高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。局或乙连胜高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。局时，第二局赛完时比赛结束．

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．   解得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，  高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．…5分                            

    （Ⅱ）依题意知，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的所有可能值为2，4，6．       

    设每两局比赛为一轮，则该轮赛完时比赛结束的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    若该轮赛完时比赛还将继续，则甲、乙在该轮中必是各得1分，此时，该轮比赛结果对下轮比赛是否停止没有影响．

    从而有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，　高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。， 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。随机变量高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的分布列为：                           

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    2

    4

    6

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    …………………………………………………………………………………………10分

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   ………………………………………………12分

    19.（12分）解：（Ⅰ）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.    …………………………………………………………4分

    （Ⅱ）过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。垂足为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，垂足为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由三垂线定理得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。;

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是所求二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的平面角.……………………6分
    设，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    故所求二面角高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的度数为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．…………………………………………8分

    （Ⅲ）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,要使高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,由三垂线定理可知，只需高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为菱形，此时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,要使高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中点，只需高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为正三角形，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,且点D落在BC上，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即为侧棱与底面所成的角．

    故当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时， 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且使点D为BC的中点．………………12分

    20.（12分）

     解：(Ⅰ) 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    …………………………………………………………………………………………2分

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。  ……5分

    （Ⅱ）若高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图像与高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图像恰有四个不同交点，

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有四个不同的根，亦即方程高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有四个不同的根．…………………7分

    令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．…………………8分

     

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。变化时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的变化情况如下表：

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    -1

    (-1,0)

    0

    (0,1)

    1

    (1,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的符号

    +

    0

    -

    0

    +

    0

    -

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调性

    ㄊ

    极大值

    ㄋ

    极小值

    ㄊ

    极大值

    ㄋ

    由表格知：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．……10分

     

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可知，当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………12分

    21.（12分）解：(Ⅰ)由题意：点P是AB的垂直平分线与BF的交点，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        ∴P点轨迹为以A、F为焦点的椭圆.………………………………3分

     

    设方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………6分

    （Ⅱ）假设存在满足题意的直线l，若l斜率不存在，易知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    不符合题意，故其斜率存在，设为k，设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………8分

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    解得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   代入验证高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。成立

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………………………12分

    22. 解：（Ⅰ） 由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   

     ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   ……………………………………………………3分

    （Ⅱ）∵高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。， 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………7分

    （Ⅲ）由（Ⅱ）知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

                           

    法1：∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

          高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

           高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………12分

    法2：原不等式只需证： 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∵高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    

    ∴高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     

     

     


    同步练习册答案