练习册

  • 练习册
  • 试题
    1．答第Ⅱ卷前.考生务必将密封线内的项目填写清楚. 【查看更多】

     

    题目列表(包括答案和解析)

    答第I卷前，考生务必将自己的姓名、考试科目涂写在答题卡上。考试结束时，将试题卷和答题卡一并交回。

    查看答案和解析>>

    答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置。

    查看答案和解析>>

    答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、班级和考号填写在答题卷上。

    查看答案和解析>>

    （本小题共13分）若有穷数列{an}满足：（1）首项a1=1，末项am=k，（2）an+1= an+1或an+1=2an ，（n=1，2，…，m-1），则称数列{an}为k的m阶数列．

    （Ⅰ）请写出一个10的6阶数列；

    （Ⅱ）设数列{bn}是各项为自然数的递增数列，若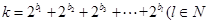，且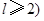，求m的最小值．

    （考生务必将答案答在答题卡上，在试卷上作答无效）

     

     

    查看答案和解析>>

    （本小题共13分）
    已知集合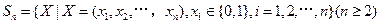对于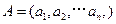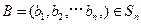，，定义A与B的差为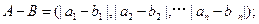

    A与B之间的距离为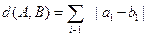
    （Ⅰ）证明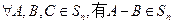：，且;
    （Ⅱ）证明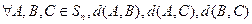：三个数中至少有一个是偶数
    (Ⅲ) 设P，P中有m(m≥2)个元素，记P中所有两元素间距离的平均值为(P).
    证明：（P）≤.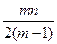
    （考生务必将答案答在答题卡上，在试卷上作答无效）

    查看答案和解析>>

    一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    B

    D

    D

    C

    A

    C

    B

    A

    C

    C

    C

    二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。

    13．13     14．       15．2           16．1005

    三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。

    17．（本小题满分12分）

    解（I）

          

      （Ⅱ）由得，

            

    18．（本小题满分12分）

    解（I）记事件A；射手甲剩下3颗子弹，

          

    （Ⅱ）记事件甲命中1次10环，乙命中两次10环，事件；甲命中2次10环，乙命中1次10环，则四次射击中恰有三次命中10环为事件

    （Ⅲ）的取值分别为16，17，18，19，20，

         

    19．(本题满分12分)

    证（Ⅰ）因为侧面，故

     在中，   由余弦定理有

      故有 

      而     且平面

         

    （Ⅱ）由

    从而  且 故

     不妨设  ，则，则

    又  则

    在中有   从而（舍负）

    故为的中点时，

     法二：以为原点为轴，设，则       由得    即

          

          化简整理得       或

         当时与重合不满足题意

         当时为的中点

         故为的中点使

     （Ⅲ）取的中点，的中点，的中点，的中点

     连则，连则，连则

     连则，且为矩形，

    又   故为所求二面角的平面角

    在中，

    法二：由已知， 所以二面角的平面角的大小为向量与的夹角

    因为  

    故

     

    20．（本小题满分12分）

    （1）由

            切线的斜率切点坐标（2，5+）

            所求切线方程为

       （2）若函数为上单调增函数，

            则在上恒成立，即不等式在上恒成立

            也即在上恒成立。

            令上述问题等价于

            而为在上的减函数，

            则于是为所求

    21．（本小题满分12分）

    解：（1），

            ∵直线l：x－y+2=0与圆x2+y2=b2相切，

    ∴=b，∴b=，b2=2，∴=3.                                                    

    ∴椭圆C1的方程是

    （2）∵MP＝MF，∴动点M到定直线l1：x＝－1的距离等于它的定点F2（1，0）的距离，

    ∴动点M的轨迹是以l1为准线，F2为焦点的抛物线，∴点M的轨迹C2的方程为。

    （3）Q（0，0），设，

    ，

    由得  ，

    ，化简得，

    当且仅当时等号成立，

    ，又∵y­22≥64，

    ∴当.    故的取值范围是.

    22．（本小题满分14分）

    解（I）由题意，令

          

     （Ⅱ）

          

      （1）当时，成立：

      （2）假设当时命题成立，即

           当时，

          

     

     

     


    同步练习册答案