练习册

  • 练习册
  • 试题
    提示:要证的结论与条件之间的联系不明显.直接由条件推出结论的线索不够清晰.另外.如果从正面证明.需要对某一个分式小于2或两个分式都小于2等进行分类讨论.而从反面证明.则只要证明两个分式都不小于2是不可能的即可.于是考虑采用反证法. 证明:假设.都不小于2.即.且. 因为..所以.且.把这两个不等式相加.得. 从而.这与已知条件矛盾.因此..都不小于2是不可能的.即原命题成立. 【查看更多】

     

    题目列表(包括答案和解析)

    已知集合A={a1，a2，…，an}中的元素都是正整数，且a1＜a2＜…＜an，对任意的x，y∈A，且x≠y，都有|x-y| ≥
    xy
    36
    ．
    （1）求证：
    1
    a1
    -
    1
    an
    ≥
    n-1
    36
    ；（提示：可先求证
    1
    ai
    -
    1
    ai+1
    ≥
    1
    36
    （i=1，2，…，n-1），然后再完成所要证的结论．）
    （2）求证：n≤11；
    （3）对于n=11，试给出一个满足条件的集合A．

    查看答案和解析>>

    已知集合A={a1，a2，…，an}中的元素都是正整数，且a1＜a2＜…＜an，对任意的x，y∈A，且x≠y，都有．
    （1）求证：；（提示：可先求证（i=1，2，…，n-1），然后再完成所要证的结论．）
    （2）求证：n≤11；
    （3）对于n=11，试给出一个满足条件的集合A．

    查看答案和解析>>

    一般地，从要证明的结论出发，逐步寻求推证过程中使每一步结论成立的　　　　　　，直至最后，把要证明的结论归纳为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做         ，用框图表示为　　　　　　　　　　　.

    查看答案和解析>>

    证明是直接从原命题的条件逐步推得命题成立的，这种证明通常称为________，其一般形式为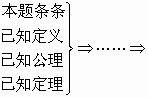本题结论．其中从已知条件出发，以已知的定义、定理、公理为依据，逐步下推，直到推出要证明的结论为止，这种证明方法称为________，推证过程为已知条件…………结论．而从问题的结论出发，追溯导致结论成立的条件，逐步上溯直到使结论成立的条件和已知条件或已知事实吻合为止，这种证明方法常称为________，推证过程为…………．

    查看答案和解析>>

    一般地，从要证明的结论出发，逐步寻求推证过程中使每一步结论成立的________，直至最后，把要证明的结论归纳为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止，这种证明的方法叫做________，用框图表示为________．

    查看答案和解析>>


    同步练习册答案