
题目列表(包括答案和解析)
2009年5月11日,中国内地出现首例输入性甲型H1N1流感疑似病例。中国进入防控甲型H1N1流感的关键时期,到目前为止,中国在防控方面取得了令人满意的成绩。据统计:公众对我国防控甲型H1N1流感的满意率![]() ,(不满意率为
,(不满意率为![]() ,
,![]() ),现随机从人群中抽出
),现随机从人群中抽出![]() 个人调查对我国防控甲型H1N1流感的满意度,用随机变量
个人调查对我国防控甲型H1N1流感的满意度,用随机变量![]() 表示调查的这些人中的不满意的人数.
表示调查的这些人中的不满意的人数.
(1)当![]() ,
,![]() ,列出随机变量
,列出随机变量![]() 的分布列,并求出随机变量
的分布列,并求出随机变量![]() 的数学期望
的数学期望![]() ;
;
(2)试证明:![]() =
=![]() .
.
当n=1, 2, 3, 4, 5时,f(n)=n2+n+41的值分别是43,47,53,61,71,它们都是素数,由归纳法你能得到的猜想是
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
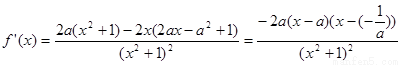 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当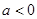 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 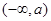 ,
,

 ,
, 
【必做题】2009年5月11日,中国内地出现首例输入性甲型H1N1流感疑似病例。中国进入防控甲型H1N1流感的关键时期,到目前为止,中国在防控方面取得了令人满意的成绩。据统计:公众对我国防控甲型H1N1流感的满意率![]() ,(不满意率为
,(不满意率为![]() ,
,![]() ),现随机从人群中抽出
),现随机从人群中抽出![]() 个人调查对我国防控甲型H1N1流感的满意度,用随机变量
个人调查对我国防控甲型H1N1流感的满意度,用随机变量![]() 表示调查的这些人中的不满意的人数.
表示调查的这些人中的不满意的人数.
(1)当![]() ,
,![]() ,列出随机变量
,列出随机变量![]() 的分布列,并求出随机变量
的分布列,并求出随机变量![]() 的数学期望
的数学期望![]() ;
;
(2)试证明:![]() =
=![]() .
.
【必做题】2009年5月11日,中国内地出现首例输入性甲型H1N1流感疑似病例。中国进入防控甲型H1N1流感的关键时期,到目前为止,中国在防控方面取得了令人满意的成绩。据统计:公众对我国防控甲型H1N1流感的满意率![]() ,(不满意率为
,(不满意率为![]() ,
,![]() ),现随机从人群中抽出
),现随机从人群中抽出![]() 个人调查对我国防控甲型H1N1流感的满意度,用随机变量
个人调查对我国防控甲型H1N1流感的满意度,用随机变量![]() 表示调查的这些人中的不满意的人数.
表示调查的这些人中的不满意的人数.
(1)当![]() ,
,![]() ,列出随机变量
,列出随机变量![]() 的分布列,并求出随机变量
的分布列,并求出随机变量![]() 的数学期望
的数学期望![]() ;
;
(2)试证明:![]() =
=![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com