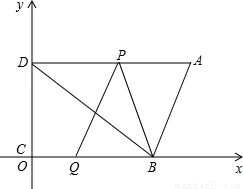
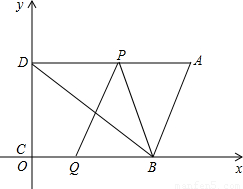
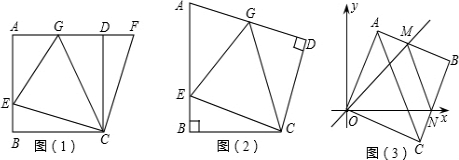
27、如图（1），在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．容易证得：CE=CF；
（1）在图1中，若G在AD上，且∠GCE=45°．试猜想GE、BE、GD三线段之间的数量关系，并证明你的结论．
（2）运用（1）中解答所积累的经验和知识，完成下面两题：
①如图（2），在四边形ABCD中∠B=∠D=90°，BC=CD，点E，点G分别是AB边，AD边上的动点．若∠BCD=α°，∠ECG=β°，试探索当α和β满足什么关系时，图（1）中GE、BE、GD三线段之间的关系仍然成立，并说明理由．
②在平面直角坐标中，边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图（3））．设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论．