例2 如图3.已知面积为1的正方形的对角线相交于点.过点O 任作一条直线分别交于.则阴影部分的面积是．解析:将△OCF绕点O旋转180°后.恰好与△OAE重合. 于是阴影部分的面积就相当于△OAD的面积.即是正方形面积的.故阴影部分面积为. 【查看更多】

18、如图所示，图形（1），（2），（3），（4）分别由两个相同的正三角形，正方形，正五边形，正六边形组成．本题中我们探索各图形顶点，边数，区域三者之间的关系．（例我们规定如图（2）的顶点数为16；边数为24，像A₁A，AH为边，AH不能再算边，边与边不能重叠；区域数为9，它们由八个小三角形区域和中间区域ABCDEFGH组成，它们相互独立．）
（1）每个图形中各有多少个顶点？多少条边？多少个区域？请将结果填入表格中．
（2）根据（1）中的结论，写出a，b，c三者之间的关系表达式．

归纳猜想：同学们，让我们一起进行一次研究性学习：
（1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？

（2）如图2将半径为R的正方形沿直线l向右翻滚，当正方形翻滚一周时，其中心O经过的路程是多少？

（3）猜想：把正多边形翻滚一周，其中心O所经过的路程是多少（R为正多边形的半径，可参看图2）？请说明理由．

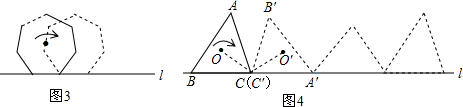
（4）进一步猜想：任何多边形都有一个外接圆，若将任意圆内接多边形翻滚一周时，其外心所经过的路程是否是一个定值（R为多边形外接圆的半径）？为什么？请以任意三角形为例说明（如图12）．
通过以上猜想你可得到什么样的结论？请写出来．

查看答案和解析>>

我们平常的数都是十进制数，表示十进制的数要用10个数码（也叫数字）：0，1，2，3，4，5，6，7，8，9．在电子计算机中用的是二进制数，只有两个数码0和1．二进制数和十进制数之间可仿照例1，例2的规律转换，例1、如二进制数101_（2）=1×2²+0×2¹+1=5，故二进制的101_（2）等于十进制的数5；例2、如二进制数10101_（2）=1×2⁴+0×2³+1×2²+0×2¹+1=21，故二进制的10101_（2）等于十进制的数21，那么二进制的110111_（2）等于十进制的数（　　）

A．54

B．55

C．56

D．57

查看答案和解析>>

归纳猜想：同学们，让我们一起进行一次研究性学习：
（1）如图1已知正三角形ABC的中心为O，半径为R，将其沿直线l向右翻滚，当正三角形翻滚一周时，其中心O经过的路程是多少？